Ответ: $\displaystyle 4 \sqrt{5}$.

Решение:

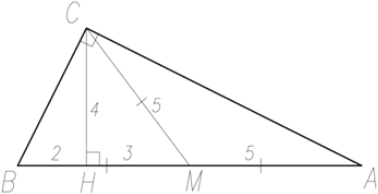
Пусть ∠ACB – прямой угол, AC – наибольший катет треугольника ABC. Пусть медиана CM = 5 и высота CH = 4.

По теореме Пифагора:

$ MH = \sqrt{CM^2 - CH^2} = \sqrt{25 - 16} = 3$.

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, поэтому:

$BH = BM − MH = 5 − 3 = 2$,

$AH = AM + MH = 5 + 3 = 8$.

Следовательно:

$ BC = \sqrt{BH \cdot AB} = \sqrt{2 \cdot 10} = 2\sqrt{5}$,

$ AC = \sqrt{AH \cdot AB} = \sqrt{8 \cdot 10} = 4\sqrt{5}$.