Решите неравенство $\left(x^2-x\right)^2+3\left(x^2-x\right)+2>0$.

Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.

Пусть $a$, $b$, $c$, $d$ - положительные числа. Вычислите $\displaystyle \frac{a^2+b^2}{c^2+d^2}$, если $a+b=b+c=c+d$.

Решить уравнение $x^2-x y-2 x+3 y=10$ в целых числах.

При каких значениях $m$ уравнение $\displaystyle \frac{2 x^2+3 x+m}{x+m}=0$ имеет ровно один корень?

Медиана и высота прямоугольного треугольника, проведённые из вершины прямого угла, равны 5 и 4. Найдите наибольший катет.

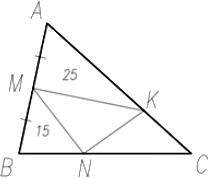
На сторонах AB, BC и AC треугольника ABC, площадь которого равна 75, расположены точки M, N и K соответственно. Известно, что M – середина AB, площадь треугольника BMN равна 15, а площадь треугольника AMK равна 25. Найдите площадь треугольника CNK.