Задача 7.
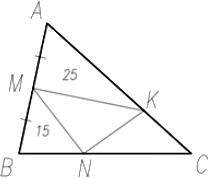
На сторонах AB, BC и AC треугольника ABC, площадь которого равна 75, расположены точки M, N и K соответственно. Известно, что M – середина AB, площадь треугольника BMN равна 15, а площадь треугольника AMK равна 25. Найдите площадь треугольника CNK.
Ответ на Задачу 7.
Ответ: 15.
Решение:
Обозначим $S_{\triangle A B C}=S$.
Toгдa $\displaystyle \frac{S_{\triangle A M K}}{S}=\frac{A M}{A B} \cdot \frac{A K}{A C}=\frac{1}{2} \cdot \frac{A K}{A C}$,
а т.к. по условию задачи $\displaystyle \frac{S_{\triangle A M K}}{S}=\frac{25}{75}=\frac{1}{3}$, то $\displaystyle \frac{1}{2} \cdot \frac{A K}{A C}=\frac{1}{3}$,
откуда находим, что $\displaystyle \frac{A K}{A C}=\frac{2}{3}$, а $\displaystyle \frac{C K}{A C}=\frac{1}{3}$.
Аналогично находим, что $\displaystyle \frac{C N}{B C}=\frac{3}{5}$.
Следовательно, $\displaystyle S_{\triangle C N K}=\frac{C K}{A C} \cdot \frac{C N}{B C} \cdot S=\frac{1}{3} \cdot \frac{3}{5} \cdot 75=15$.

