Открытая интернет-олимпиада по математике Меташколы, 9 класс, 2021 год, 2 этап
дата проведения: 26 января 2021
источник: https://vivat2.okis.ru/metashkola
Задача 6.
Две окружности радиусов 4 и 3 с центрами в точках O1 и О2 касаются некоторой прямой в точках М1 и М2 соответственно и лежат по разные стороны от этой прямой. Отношение отрезка O1O2 к отрезку М1М2 равно $ 2/\sqrt3 $. Найдите O1O2.
Ответ на Задачу 6.
Ответ: 14.
Решение:
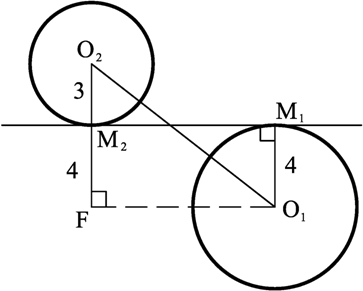
Опустим перпендикуляр O1F из центра первой окружности на продолжение радиуса O2M2 второй окружности. Тогда О1F = М1М2 , М2F = O1M1 = 4 , O2F = О2М2 + M2F = 3 + 4 = 7.
Из прямоугольного треугольника О1FО2 :
cos∠FO1O2 = O1F / О1О2 = М1М2 / О1О2 = $ \sqrt3/2 $, значит, ∠FO1O2 = 30°. Следовательно, О1О2 = 2⋅О2F = 2⋅7 = 14.
