Открытая интернет-олимпиада по математике Меташколы, 9 класс, 2021 год, 2 этап
дата проведения: 26 января 2021
источник: https://vivat2.okis.ru/metashkola
Задача 7.
Внутри угла BOA лежит точка М, ∠BOM = 25°, ∠MOA = 40°, MB⊥OB, MA⊥OA. Найти угол AMB (в градусах).
Ответ на Задачу 7.
Ответ: 115°.
Решение:
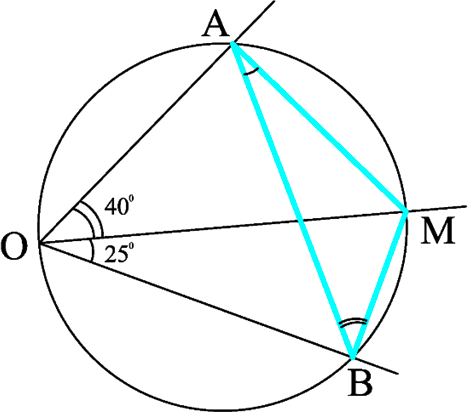
∠OBM + ∠OAM = 180°, следовательно, точки О, В, М, А лежат на одной окружности.
∠ABM = ∠AOM = 40°,
∠BAM = ∠BOM = 25° как вписанные углы, опирающиеся на соответственно равные дуги.
Значит, ∠AMB = 180° − 40° − 25° = 115°.
