Задача 1.
Уменьшите число 12345 на столько единиц, сколько целых сотен содержится в данном числе.
Задача 2.
Купец Савватий рассчитал, что на все имеющиеся при нём деньги он может закупить или 16 одинаковых рубах, или 10 одинаковых пар сапог, причём после покупки рубах или сапог ни копейки не останется. Одна пара сапог стоит на три рубля дороже одной рубахи. Сколько у Савватия денег?
Задача 3.
Лиса встала первой. За ней встал заяц, за ним — волк, потом — медведь, потом — енот. Каждый, кто стоял на втором и на четвёртом месте, в том же порядке (сначала второй, потом четвёртый) встали в конец строя. Потом опять каждый, кто теперь стоял на втором и на четвёртом месте, в том же порядке встали в конец строя. И, наконец, ещё раз каждый, кто теперь стоял на втором и на четвёртом месте, в том же порядке встали в конец строя. Напишите, кто на каком месте теперь стоит.
Задача 4.
На некоторых табличках написана правда. Обведите эти таблички. Объясните свой выбор.

Задача 5.
У Бабы Яги есть волшебные сундуки (вид сверху):
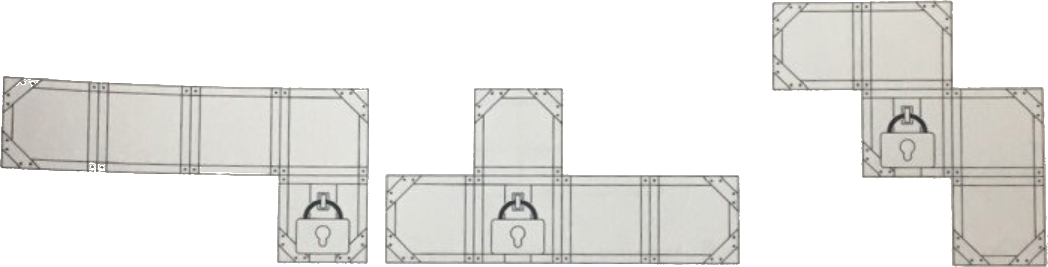
Нарисуйте по клеточкам плащ-невидимку, под которым можно спрятать любой сундук. Используйте как можно меньше клеточек. Чтобы спрятать сундук, надо накрыть плащом его крышку.
Задача 6.
На столе лежит вот такая бумажная таблица:
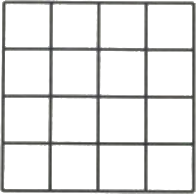
Степан разложил несколько ключиков в клетки этой таблицы. Ефим берёт 4 вот такие полоски (он их не поворачивает):
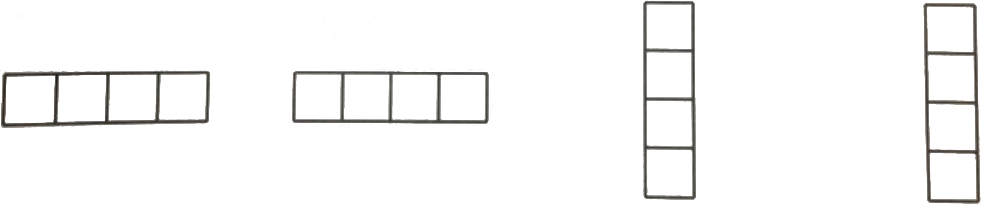
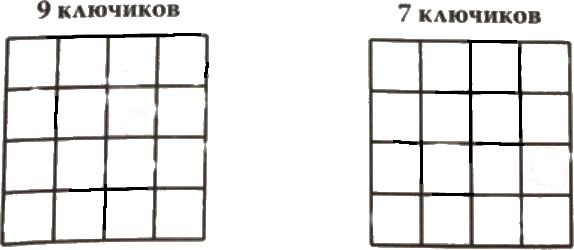
Как бы Ефим их ни положил на таблицу, хотя бы один ключик всегда видно. На левом рисунке покажите, как Степан разложил ключики, если у него их 9. На правом рисунке покажите, как Степан сделал это, если у него их 7.
Задача 7.
! Задача была снята по причине чрезмерной сложности !
Рабочий выложил бесконечную мозаику из одинаковых треугольников. Фрагмент мозаики представлен на рисунке ниже:
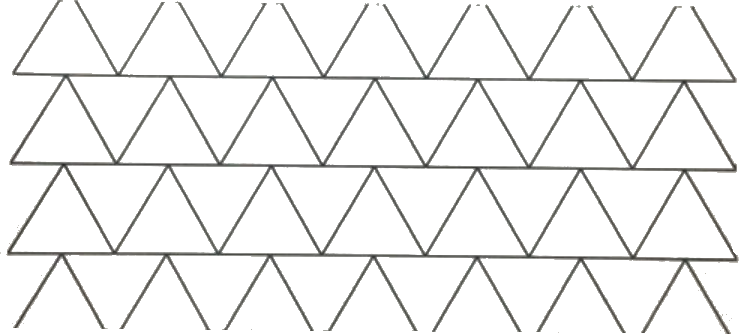
Раскрасьте треугольники в три цвета так, чтобы выполнялось два условия (вместо раскраски Вы можете просто расставить в треугольниках цифры 1, 2, 3):
- треугольники одинакового цвета могут граничить только по вершине (или не граничить вообще);
- если убрать все треугольники любого цвета, то из любого треугольника одного из оставшихся цветов можно будет попасть в любой оставшийся треугольник, переходя в соседний через сторону или, может быть, её часть (но не через вершину).

