Задача 7.
! Задача была снята по причине чрезмерной сложности !
Рабочий выложил бесконечную мозаику из одинаковых треугольников. Фрагмент мозаики представлен на рисунке ниже:
Раскрасьте треугольники в три цвета так, чтобы выполнялось два условия (вместо раскраски Вы можете просто расставить в треугольниках цифры 1, 2, 3):
- треугольники одинакового цвета могут граничить только по вершине (или не граничить вообще);
- если убрать все треугольники любого цвета, то из любого треугольника одного из оставшихся цветов можно будет попасть в любой оставшийся треугольник, переходя в соседний через сторону или, может быть, её часть (но не через вершину).
Ответ на Задачу 7.
Ответ: пример:

Решение:
Заметим, что нельзя раскрасить целый ряд треугольников в один цвет, как на рисунке ниже:
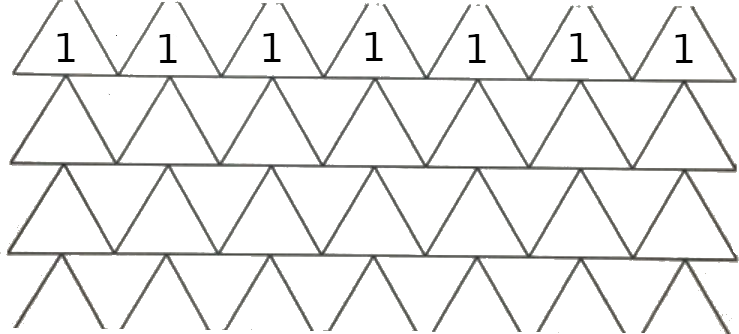
потому что тогда не будет выполняться второе условие. Ведь если мы уберём весь этот ряд (т.е. все треугольники цвета 1), то вся мозаика распадётся на две отдельные части, и данное условие не будет выполнено.
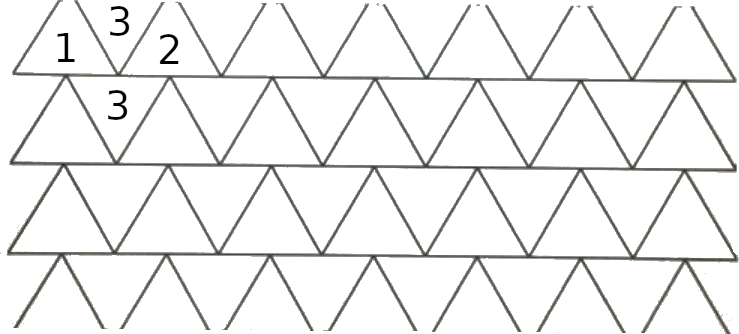
Значит, есть место в мозаике, где в ряду два разных цвета рядом. Пусть это цвета 1 и 2. Тогда перевёрнутый треугольник между ними и треугольник под ним должны быть третьего цвета, т.к. каждый из этих треугольников имеет общую границу с треугольниками 1 и 2:
Далее, обозначим некоторые треугольники с неизвестными цветами буквами:
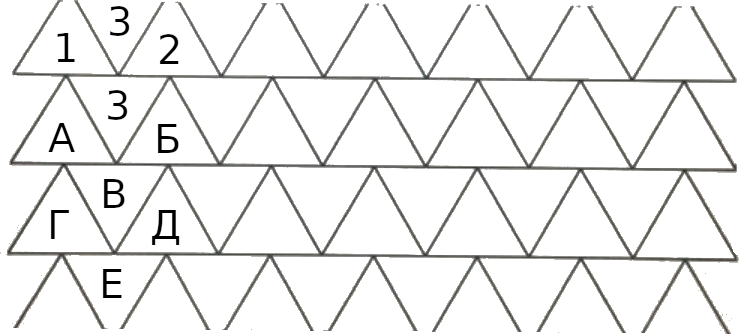
Треугольники А и Б могут быть цветов 1 и 2, 2 и 1, 1 и 1 или 2 и 2 (не могут быть цвета 3).
Если треугольники А и Б разных цветов, то треугольник В обязательно цвета 3. Если треугольники Г и Д разных цветов, то треугольник Е цвета 3. То есть, тогда мы приходим к повторению картинки по вертикали, цвет 3 повторяется. Но мы не можем бесконечно повторять вниз и вверх эту картинку по вертикали, т.к. тогда получим бесконечную вертикаль цвета 3, что также разобьёт всю мозаику на две части. Значит, в какой-то момент в паре треугольников А-Б, Г-Д, ... появятся треугольники одного цвета. Пусть это цвет 1. И тогда перевёрнутый треугольник под ними будет не цвета 3, а цвета 2:
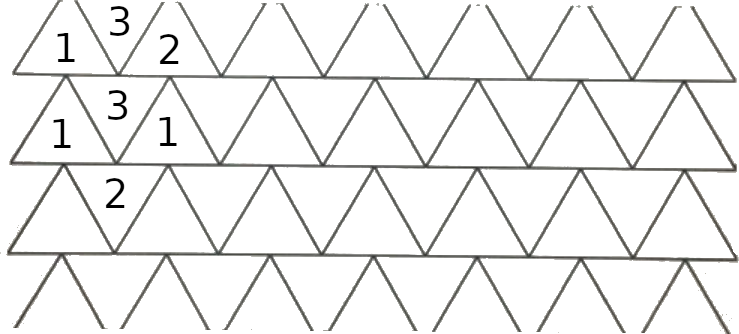
Покрасим ещё в цвет 3 треугольник, который не может быть другого цвета:
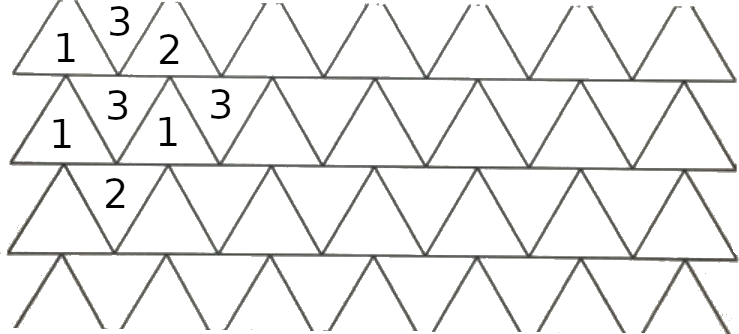
На этом этапе уже можно заметить закономерность: два треугольника по горизонтали и по вертикали одного цвета, затем цвет меняется.
Осталось проверить, что выполняются оба условия, а также доказать единственность раскраски.

