Олимпиада «Осенний Олимп», 7-9 класс, 2020 год
дата проведения: 23 октября 2020
источник: https://t.me/matolimp/443
Задача 2.
Фермер Ефим рисовал на клетчатой бумаге план загонов для скота. По линиям сетки он обвёл три области:
- область площади не менее 3 клеток
- другая область площади не менее 6 клеток
- ещё одна область площади не менее 7 клеток
Отметьте три области с как можно меньшей общей длиной границы:
Примечание: области должны быть связными: это означает, что из любой клетки области можно добраться до любой другой, перешагивая через общие стороны клеток.
Ответ на Задачу 2.
Ответ: Наименьшая суммарная длина равна 23.
Решение:
Ефим отметил три области общей площадью 3 + 6 + 7 = 16 клеток. Значит, наименьший внешний периметр будет, если из областей сложить квадрат 4 × 4.
- Форма области площадью 3 клетки не имеет значения, т.к. в любом случае у неё будет периметр 8.
- Область площадью 6 клеток имеет наименьший периметр, если это прямоугольник 2 × 3, тогда у этой области будет периметр 10.
- Область площадью 7 клеток имеет наименьший периметр 12 (это может быть прямоугольник без одной клетки или квадрат без двух клеток).
Добавим внешний периметр квадрата 4 × 4 (он равен 16) и учтём, что каждая граница принадлежит двум клеткам, тогда получим наименьшую возможную длину общей границы: (8 + 10 + 12 + 16) / 2 = 23.
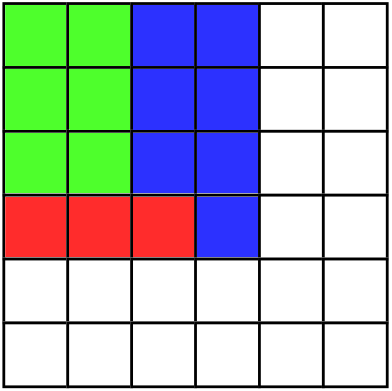
Пример загона с длиной границы 23:
