Ровно в четверти всех хозяйств посёлка Н имеется не менее трёх коров в каждом. Ещё в четверти всех хозяйств по две коровы в каждом. В каждом из остальных хозяйств по одной корове. Всего коров в посёлке 17.

Сколько в посёлке Н могло быть хозяйств? Укажи все варианты.

Фермер Ефим рисовал на клетчатой бумаге план загонов для скота. По линиям сетки он обвёл три области:

• область площади не менее 3 клеток
• другая область площади не менее 6 клеток
• ещё одна область площади не менее 7 клеток

Отметьте три области с как можно меньшей общей длиной границы:

Примечание: области должны быть связными: это означает, что из любой клетки области можно добраться до любой другой, перешагивая через общие стороны клеток.

Петя и Вася спорят о своих «успехах» в школьной математике:

• Петя: «У тебя на пять двоек больше, чем у меня!»
• Вася: «А у тебя на две пятёрки меньше, чем у меня!»
• Петя: «Нет, у нас одинаковое количество пятёрок!»
• Вася: «У нас одинаковое количество четвёрок!»
• Петя: «Но у меня три четвёрки, а у тебя всего одна!»
• Вася: «Зато у нас одинаковая сумма всех оценок!»
• Петя: «Общее количество наших пятёрок нечётно!»
• Вася: «А у тебя больше десяти троек!»

Известно, что у каждого из мальчиков правдивые и ложные высказывания чередовались через одно: за каждым правдивым высказыванием следовало ложное, а за ложным — правдивое. Также известно, что никаких оценок, кроме двоек, троек, четвёрок и пятёрок, у мальчиков нет.

Какое наибольшее количество троек могло быть у Васи?

Несколько гусар сидят за круглым столом и играют в карты. Правила простые: первым ходом на стол нужно положить одну карту. Далее каждым ходом нужно положить на стол на одну карту больше, чем положил предыдущий сходивший игрок. Игра заканчивается тогда, когда кто-то не может сделать очередной ход.

Поручик Ржевский заметил, что первый ход сделал корнет Оболенский. Следующий ход сделал правый сосед правого соседа Оболенского. И так продолжалось весьма долго: очередной ход делал правый сосед правого соседа последнего сходившего. По окончанию игры нашлись три соседа, самый левый из которых суммарно выложил 30 карт, средний — 21 карту, а самый правый — 33.

Сколько гусар могло быть за столом? Укажите все варианты.

После окончания богатырского турнира участники разъехались по восьми направлениям розы ветров:

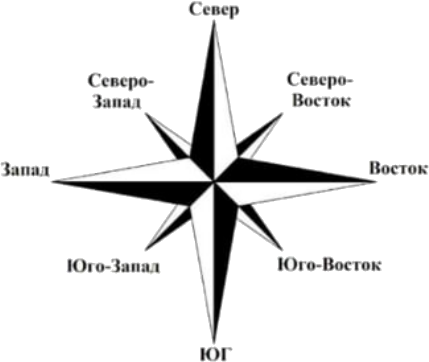
причём в каждом направлении отбыл хотя бы один человек.

Во все северные направления отбыло не более 28% богатырей, во все восточные — не более 25%, во все южные — не более 25%, и не более 25% уехали строго на запад.

Всего богатырей было не более 70. Сколько богатырей могло быть на турнире?

Задача была снята из-за некорректности условия (отсутствия модели, в которой все объёмы неотрицательны).

Три тортика, пирожное и три горшочка с мёдом успешно помещаются в Винни-Пуха. А вот тортик, два пирожных и пять горшочков с мёдом Винни-Пух уже не осилит. Как и четыре тортика, да ещё две трети тортика, да горшочек с мёдом.

Какое наибольшее (целое) количество тортиков может съесть Винни-Пух за один присест?

Доярка Авдотья, работая в коровнике, увидела большую тучу и побежала в дом. Когда она была на половине дистанции, её увидела доярка Прасковья, работавшая в этот момент в том же коровнике, и тоже побежала в дом. В итоге доярки добежали до дома с интервалом в 200 секунд, а за 50 секунд до того, как первая из доярок вбежала в дом, расстояние между доярками равнялось расстоянию от дома до ближайшей доярки.

Найдите возможные скорости доярок, если от коровника до дома 1 километр.

Выдающийся счетовод Ефим считает тройку различных целых положительных чисел интересной, если разность какой-то пары этих чисел составляет треть оставшегося и разность какой-то другой пары этих чисел составляет треть оставшегося.

Сколько существует интересных троек с суммой, не превышающей 2020?