Задача 3.
Замени буквы на цифры так, чтобы получилось верное равенство:
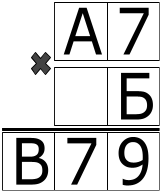
Ответ на Задачу 3.
Единственное решение А = 9, Б = 7, В = 6 можно найти аккуратным перебором. Мы же покажем, как это можно сделать почти без перебора (но потребуется некоторое умение манипулировать с буквенными выражениями).
Условие задачи можно записать так:
(10⋅А + 7)⋅Б = В⋅100 + 79
Это можно переписать как:
10⋅(А⋅Б – 10⋅В) = 7⋅(11 − Б) + 2
Запись значения правой части должна заканчиваться на 0. Это означает, что 7⋅(11 − Б) должно заканчиваться на 8. Так бывает только когда Б = 7 и, соответственно:
7⋅А − 10⋅В = 3
что можно переписать как:
10⋅В = 7⋅А − 3
Запись значения правой части должна заканчиваться на 0. Это означает, что 7⋅А должно заканчиваться на 3. Так бывает только когда А = 9 и, соответственно, В = 6.

