Задача 8.
На конференцию съехались девять человек. Каждый из них либо торговец (торговцы всегда врут), либо исследователь (исследователи всегда говорят правду). Всех их расселили в гостинице по одному в комнату. Сегодня утром каждый из заселившихся сказал: «Среди моих соседей исследователей больше, чем торговцев».
Гостиница имеет следующую планировку (на единственном этаже девять одинаковых квадратных комнат):
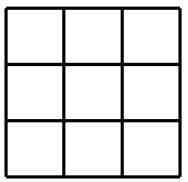
Сколько торговцев могло быть на конференции, если каждый гость в точности знал, кто именно его соседи?
Комментарий: Соседями считаются жильцы комнат с общей стеной. Нужно найти все возможные варианты ответа.
Ответ на Задачу 8.
Предположим, что в левой верхней клетке исследователь:
И ? ?
? ? ?
? ? ?
Тогда оба его соседа — исследователи:
И И ?
И ? ?
? ? ?
Если по центру торговец, то два оставшихся его соседа — торговцы:
И И ?
И Т Т
? Т ?
При этом в правой верхней клетке должен быть торговец, но тогда у центрального верхнего исследователя получается два соседа-торговца. Поэтому такой вариант не реализуется.
Если же по центру исследователь, то у него есть ещё хотя бы один сосед-исследователь. Будем считать (без ограничения общности), что расселение имеет следующий вид:
И И ?
И И И
? ? ?
Имеем две ситуации. Первая: центральный нижний — исследователь. Тогда и угловые — исследователи:
И И И
И И И
И И И
Вторая: центральный нижний — торговец. Тогда его оставшиеся соседи — торговцы, а верхний правый — по-прежнему исследователь:
И И И
И И И
Т Т Т
Мы доказали, что если в какой-то угловой клетке есть исследователь, то торговцев 0 или 3.
Рассмотрим теперь ситуацию, когда во всех угловых клетках торговцы:
Т ? Т
? ? ?
Т ? Т
Но тогда в центральных клетках всех сторон находятся торговцы. А следовательно, и в центре — торговец. Получилось 9 торговцев.
Ответ: торговцев 0, 3 или 9.

