Задача 5. Робот-пылесос
Современные роботы-пылесосы очень умные. Например, они способны в своей памяти строить карту помещения, разбивать помещение на сектора и даже прогнозировать загрязнения каждого сектора. Сектора, закрашенные в чёрный цвет, недоступны для уборки. Там, вероятно, стоит диван, кресло или какое-то другое препятствие. Число на секторе — это прогнозируемое количество пыли. У робота-пылесоса, который отмечен на карте помещения рисунком, заканчивается заряд батареи, и пылесос может выполнить только X перемещений в соседний сектор. По какому маршруту лучше пройти роботу, чтобы собрать как можно больше пыли?
Карта помещения:
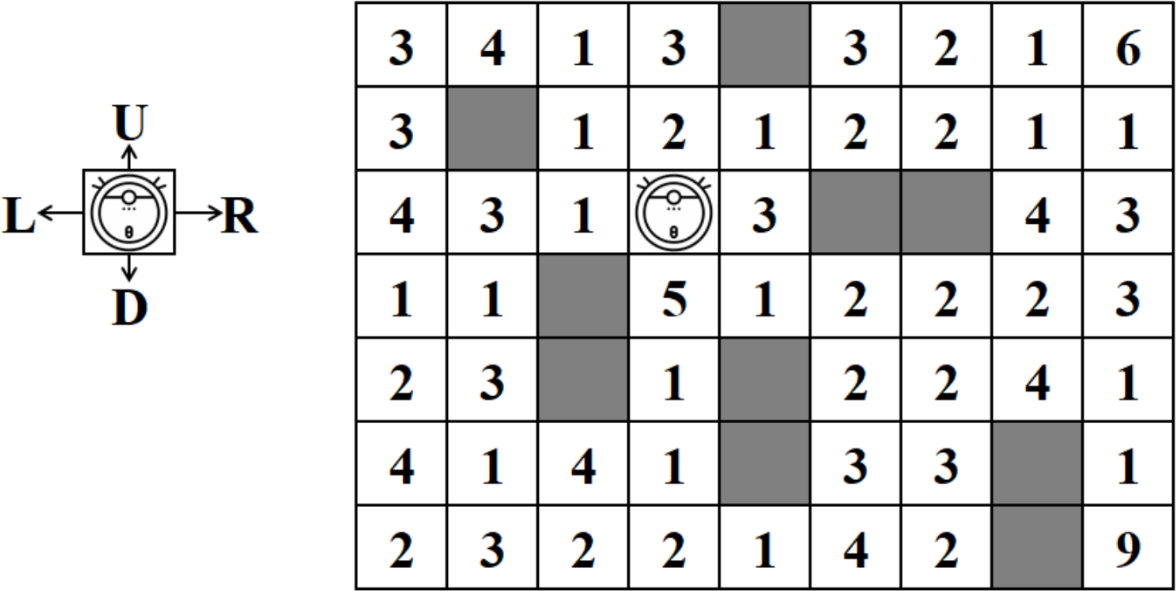
Робот-пылесос может передвигаться строго по свободным секторам (не покрашенным в чёрный цвет) и не может выезжать за пределы помещения. Если пылесос сталкивается с препятствием или стеной комнаты, то он останавливается.
Маршрут пылесоса необходимо записать в виде строки из символов «U», «D», «L», «R», где «U» обозначает перемещение на один сектор вверх, «D» — перемещение вниз, «L» — перемещение влево, «R» — перемещение вправо.
Например, при движении по маршруту «URR» робот-пылесос соберёт 5 единиц пыли, а при исполнении маршрута «RRU» соберёт 3 единицы пыли, затем столкнётся с препятствием и остановится.
Запишите маршрут движения робота-пылесоса, при котором он сможет собрать наибольшее количество пыли при заданных X. Ответы записывайте в виде последовательностей символов «U», «D», «L», «R» без пробелов и иных разделителей.
Ответ на Задачу 5.
Решение 1.
Решение основывается на переборе разных вариантов маршрутов, где мы стремимся набрать как можно больше пыли.
Маршруты легче искать в такой таблице, если закрасить сектора в разные цвета в зависимости от количества пыли. Это легко можно сделать в электронных таблицах: нужно переписать данные в таблицу, выделить её и применить «Условное форматирование» —> «Цветовые шкалы» —> «Цветовая шкала зелёный-жёлтый-красный». Теперь маленькие числа будут красными, а большие — зелёными. Такая таблица называется тепловой картой.
Тепловая карта помещения:
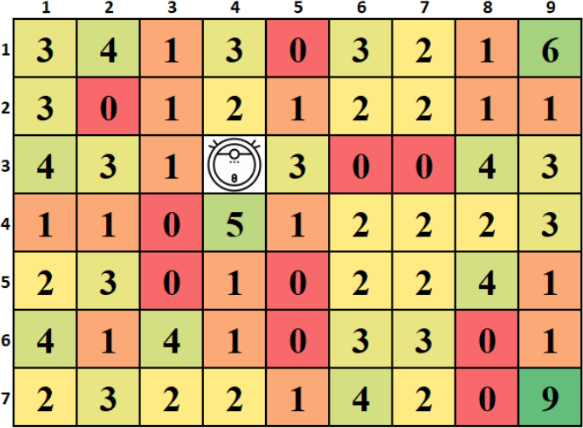
Найдём решение для X = 3:
В радиусе трёх секторов от робота-пылесоса самые большие числа — это 5, 4 и несколько троек. Попытаемся их объединить и найти маршрут, который позволит роботу собрать наибольшее количество пыли.
- LLL 1 + 3 + 4 = 8
- DRU 5 + 1 + 3 = 9
- RDL 3 + 1 + 5 = 9
Остальные маршруты позволят собрать намного меньше пыли То есть наилучший маршрут позволяет собрать 9 единиц пыли и будет иметь вид «DRU» или «RDL». Пример маршрута «RDL»:
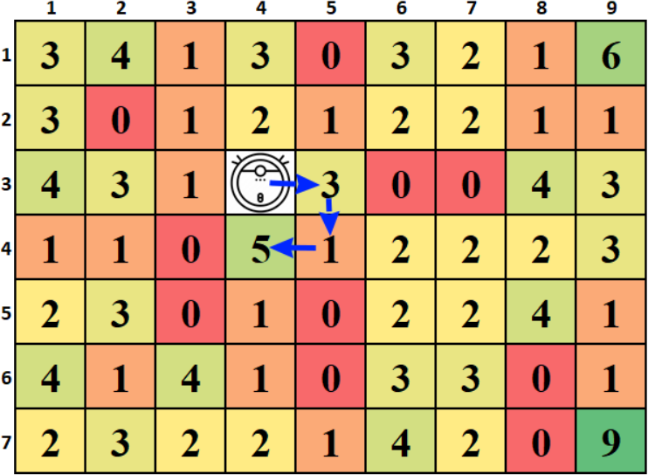
Для нахождения ответа при X = 5, 7, 9 используем аналогичную логику. Определяем области секторов, где мы можем набрать больше всего пыли, и строим маршрут туда через сектора с наибольшими числами.
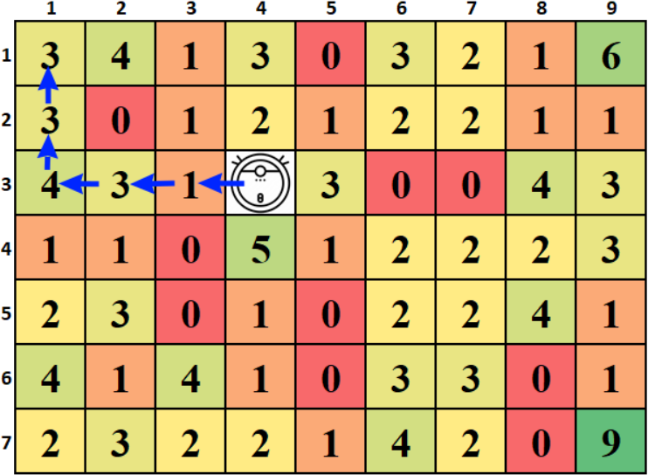
Для X = 5 маршрут «LLLUU» позволяет собрать 14 единиц пыли.
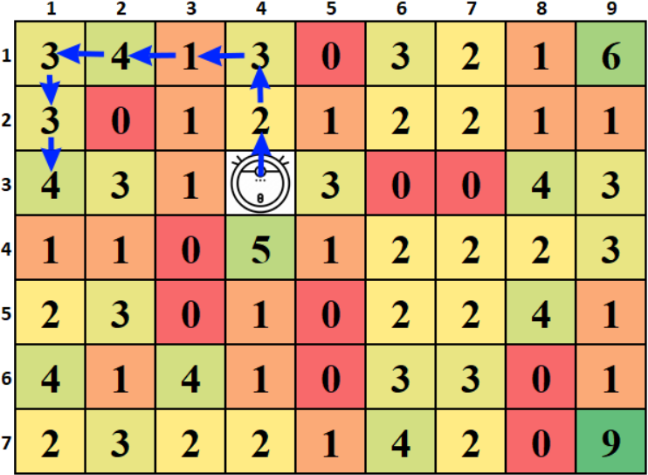
Для X = 7 маршрут «UULLLDD» позволяет собрать 20 единиц пыли.
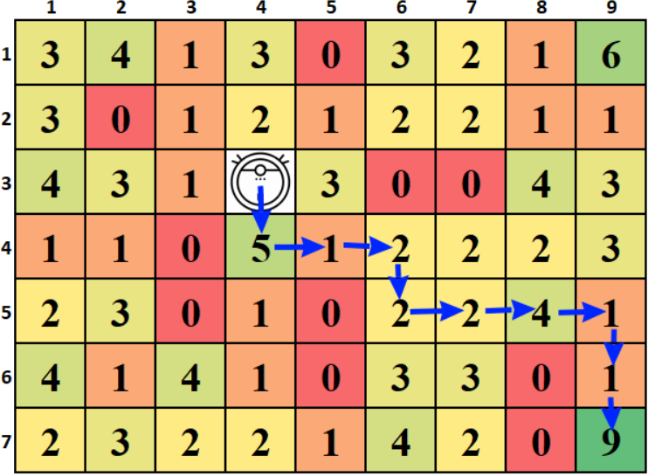
Для X = 9 маршрут «DRRDRRRDD» позволяет собрать 27 единиц пыли.
Решение 2.
Ещё один способ решения — написать программу, которая переберёт все маршруты нужной длины и найдёт маршрут, позволяющий собрать больше всего пыли. Полный перебор можно реализовать через рекурсивный алгоритм поиска в глубину. Такое решение в данной задаче будет работать довольно быстро, потому что маршрут максимальной длины не очень длинный.
x, y = 2, 3 # начальная координата робота
n, m = 7, 9 # размеры помещения
# карта помещения. Препятствия заменены на -99,
# чтобы роботу было явно невыгодно туда ходить
field = [[ 3, 4, 1, 3, -99, 3, 2, 1, 6 ],
[ 3, -99, 1, 2, 1, 2, 2, 1, 1 ],
[ 4, 3, 1, 0, 3, -99, -99, 4, 3 ],
[ 1, 1, -99, 5, 1, 2, 2, 2, 3 ],
[ 2, 3, -99, 1, -99, 2, 2, 4, 1 ],
[ 4, 1, 4, 1, -99, 3, 3, -99, 1 ],
[ 2, 3, 2, 2, 1, 4, 2, -99, 9 ]]
# двумерный список, где мы будем отмечать сектора, по которым
# проехал робот-пылесос. 0 − не проехал, 1 − проехал
used = [ [0] * m for _ in range(n) ]
# из любого сектора можно проехать в одну из четырёх сторон (список направлений).
# 0. y - 1, x + 0 − движение вверх (U)
# 1. y + 1, x + 0 − движение вниз (D)
# 2. y, x - 1 − движение влево (L)
# 3. y, x + 1 − движение вправо (R)
d = [[ -1, 0], [1, 0], [0, -1], [0, 1]]
# функция, которая проверяет, находится ли робот-пылесос внутри помещения
def coord_ok(i, j):
return 0 < = i < n and 0 < = j < m
# функция рекурсивного перебора.
# i, j − текущая координата робота
# curEnergy − количество потраченного заряда
# curPoints − объём собранной пыли
# bp − путь, пройденный до текущей координаты
def dfs(i, j, curEnergy, curPoints, bp):
# если заряд закончился, заканчиваем движение
if curEnergy = = energy:
return curPoints, bp
maxPoints = 0
bestPath = ""
# отправим робота на 4 разные стороны и посмотрим,
# откуда он принесёт больше всего пыли.
for k in range(4):
i1 = i + d[k][0]
j1 = j + d[k][1]
if coord_ok(i1, j1):
x = field[i1][j1]
field[i1][j1] = 0
points, path = dfs(i1, j1, curEnergy + 1, curPoints + x, bp + str(k))
if points > maxPoints:
maxPoints = points
bestPath = path
field[i1][j1] = x
return maxPoints, bestPath
# переберём длины маршрутов и для каждого случая найдём маршрут,
# который позволит роботу собрать наибольшее количество пыли.
for i in 3, 5, 7, 9:
energy = i
a, b = dfs(x, y, 0, 0, "")
# заменим номера направлений на буквы.
print(b.replace("0", "U").replace("1", "D").replace("2", "L").replace("3", "R")) 
