Задача 3.
Один из углов трапеции равен 60°. Найдите отношение её оснований, если известно, что в эту трапецию можно вписать окружность и около этой трапеции можно описать окружность.
Ответ на Задачу 3.
Ответ: 1:3
Решение:
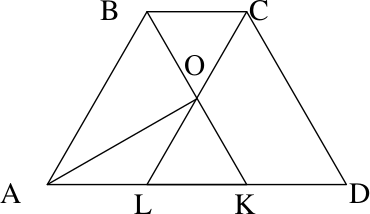
Так как $ABCD$ вписанная, то она равнобедренная, т.е. $AB$ = $CD$. Так как $∠BAD$ = 60°, то $∠ABC$ = 120°.
Центр вписанной окружности лежит в точке $O$ пересечения биссектрис $BK$ и $AO$ углов $BAD$ и $ABC$. Т.к. $∠ABK$ = 60° = $∠BAK$, то треугольник $ABK$ — равносторонний, значит, биссектриса $AO$ является медианой в этом треугольнике. Биссектриса $CL$ угла $BCD$ также проходит через точку $O$. А так как $O$ — середина $BK$, то $OL$ — средняя линия треугольника $ABK$ (проходит через середину $BK$ и параллельно $AB$), следовательно $AL$ = $LK$. Аналогично $LK$ = $KD$.
Треугольники $BCO$ и $LKO$ — правильные (углы по 60°) и их стороны равны ($BO$ = $OK$), следовательно $BC$ = $LK$ = $AL$ = $KD$, т.е. 3$BC$ = $AD$.

