Задача 6.
Прямоугольную доску покрасили в три цвета, как показано на рисунке (угловую клетку покрасили в первый цвет, две соседние с ней — во второй, три соседние с только что покрашенными — в третий, следующие соседние с уже покрашенными — снова в первый и т.д.). Может ли для каких-нибудь размеров доски случиться так, что клеток одного цвета будет на две больше, чем какого-то другого?
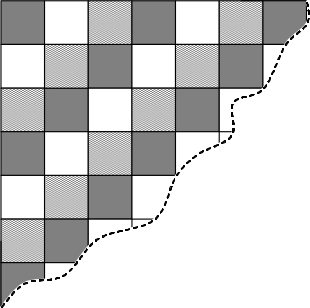
Ответ на Задачу 6.
Ответ: Нет.
Решение:
Пусть размеры доски $n$ × $m$. Будем отрезать от прямоугольника части, в которых всех цветов поровну. При такой раскраске в любом прямоугольнике 3 × 1 есть клетки всех цветов, значит в любой полоске 3$k$ × 1 всех цветов поровну.
Пусть $n$ при делении на 3 даёт остаток $r$: $n$ = 3$t$ + $r$. Отрежем от исходного прямоугольника кусок 3$t$ × m — в этом куске всех цветов поровну. Остался прямоугольник $r$ × m.
Пусть $n$ при делении на 3 даёт остаток $q$: $m$ = 3$s$ + $q$. Отрежем от оставшегося прямоугольника $r$ × m кусок $r$ × 3$s$ — в нём всех цветов поровну. Остался прямоугольник $r$ × $q$. Т.к. $r$ и $q$ — остатки при делении на 3 (т.е. числа 0, 1, 2), то всевозможные варианты для оставшегося прямоугольника — это:
- ничего не осталось, т.е. в исходном прямоугольнике клеток всех цветов поровну.
- остался прямоугольник 1 × 2. Т.к. в нём присутствуют два цвета, то в исходном прямоугольнике клеток какого-то одного цвета на одну меньше, чем клеток каждого из двух других цветов.
- остался прямоугольник 2 × 2. При нашей раскраске в нём будет одна клетка какого-то одного цвета, две — другого и одна — третьего. Т.е. в исходном прямоугольнике клеток какого-то одного цвета на одну больше, чем клеток каждого из двух других цветов.
Итак, во всех возможных вариантах получается, что максимальный разрыв между количеством клеток разных цветов равен 1.

