Задача 1.
Голова рыбы весит столько, сколько хвост и половина туловища, туловище — столько, сколько голова и хвост вместе. Хвост весит 1 кг. Сколько весит рыба?
Задача 2.
Сумма уменьшаемого, вычитаемого и разности равна 555. Может ли уменьшаемое быть целым числом? Если да, то приведите пример, если нет, то объясните, почему.
Задача 3.
В психиатрической больнице есть главный врач и много сумасшедших. В течение недели каждый сумасшедший один раз в день кусал кого-нибудь (возможно и себя). В конце недели оказалось, что у каждого из больных по два укуса, а у главного врача — сто укусов. Сколько сумасшедших в больнице?
Задача 4.
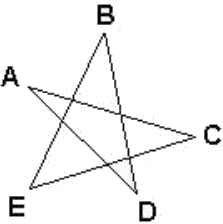
В пятиугольной звезде, изображённой на рисунке, $∠ACE$ = $∠ADB$ и $∠DBE$ = $∠BEC$. Известно также, что $BD$ = $CE$. Докажите, что $∠ACD$ = $∠ADC$.
Задача 5.
Дан числовой ребус: ТЭТА + БЭТА = ГАММА. (Разным буквам соответствуют разные цифры, одинаковым — одинаковые.) Найдите все его решения и докажите, что других нет.
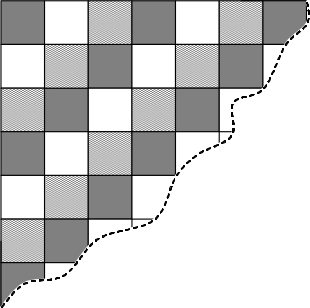
Задача 6.
Прямоугольную доску покрасили в три цвета, как показано на рисунке (угловую клетку покрасили в первый цвет, две соседние с ней — во второй, три соседние с только что покрашенными — в третий, следующие соседние с уже покрашенными — снова в первый и т.д.). Может ли для каких-нибудь размеров доски случиться так, что клеток одного цвета будет на две больше, чем какого-то другого?