Всероссийская олимпиада школьников по математике, 9 класс, 2012 год
дата проведения: 19 октября 2012 - 30 октября 2012
Задача 2.
Вася вырезал из картона треугольник, разрезал его на два треугольника и послал обе части Пете, который опять сложил из них треугольник. Верно ли, что Петин треугольник обязательно равен вырезанному Васей? Если нет — приведите пример, если да — обоснуйте.
Ответ на Задачу 2.
Ответ: Нет.
Решение:
Например, если Вася разрезал остроугольный треугольник $ABC$ по медиане $BD$ (см. левый рисунок), а Петя сложил треугольник так, как это показано на правом рисунке.
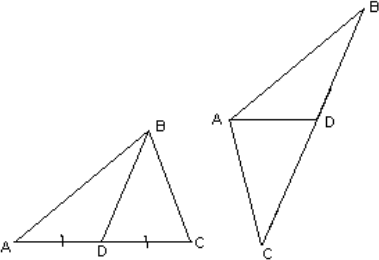
Получившийся треугольник не равен исходному, т.к. исходный — остроугольный, а получившийся — тупоугольный ($∠A$ получившегося треугольника равен сумме $∠A$ и $∠C$ исходного).

