Всероссийская олимпиада школьников по математике, 10-11 класс, 2013 год
дата проведения: 1 октября 2013 - 07 октября 2013
Задача 6.
В четырёхугольнике диагонали перпендикулярны. В него можно вписать окружность и около него можно описать окружность. Можно ли утверждать, что это квадрат?
Ответ на Задачу 6.
Ответ: Нельзя.
Решение:
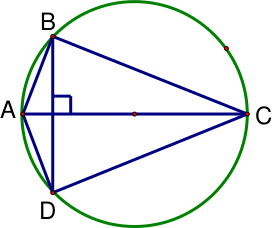
Рассмотрим в окружности диаметр $AC$ и перпендикулярную ему хорду $BD$, не проходящую через центр (см. рисунок). Покажем, что четырёхугольник $ABCD$ удовлетворяет условию задачи. Для этого достаточно доказать, что в него можно вписать окружность. В окружности диаметр делит перпендикулярную ему хорду пополам, значит, в треугольнике $BAD$ высота является медианой и этот треугольник является равнобедренным: $AB$ = $AD$. Аналогично, $CB$ = $CD$. Так как суммы противоположных сторон четырёхугольника $ABCD$ равны, в него можно вписать окружность.

