Задача 5.
В музее 16 залов, расположенных как показано на рисунке.
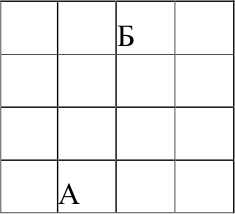
В половине из них выставлены картины, а в половине скульптуры. Из любого зала можно попасть в любой соседний с ним (имеющий общую стену). При любом осмотре музея залы чередуются: зал с картинами — зал со скульптурами — зал с картинами и т.д. Осмотр начинается в зале А, в котором висят картины, а заканчивается в зале Б.
- Обозначьте крестиками все залы, в которых висят картины.
- Турист хочет осмотреть как можно больше залов (пройти от зала А к залу Б), но при этом в каждом зале побывать не больше одного раза. Какое наибольшее количество залов он сможет посмотреть? Нарисуйте какой-нибудь его маршрут наибольшей длины и докажите, что большее количество залов он посмотреть не мог.
Ответ на Задачу 5.
Ответ: а) Смотри рисунок ниже; б) 15 залов.
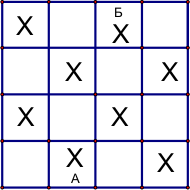
Решение:
б) Один из возможных маршрутов показан на рисунке:
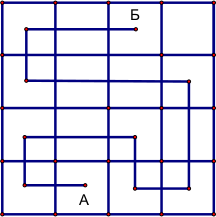
Докажем, что если турист хочет побывать в каждом зале не больше одного раза, он не сможет посмотреть больше, чем 15 залов. Заметим, что маршрут начинается в зале с картинами (А) и заканчивается в зале с картинами (Б). Значит, число залов с картинами, которые прошёл турист на один больше числа залов со скульптурами. Так как залов с картинами, которые мог пройти турист не больше 8, то залов со скульптурами — не больше 7. Итак, маршрут не может проходить больше чем через 15 залов.

