Вася может получить число 100, используя десять семёрок, скобки и знаки арифметических действий:

100 = (77 : 7 − 7 : 7) ⋅ (77 : 7 − 7 : 7)

Улучшите его результат: используйте меньшее число семёрок и получите число 100. (Достаточно привести один пример).

На часах половина девятого. Чему равен угол между часовой и минутной стрелками? (Ответ обоснуйте).

Назовём число зеркальным, если слева направо оно «читается» так же, как справа налево. Например, число 12321 — зеркальное.

1. Напишите какое-нибудь зеркальное пятизначное число, которое делится на 5.
2. Сколько существует пятизначных зеркальных чисел, которые делятся на 5?

Саша, Лёша и Коля одновременно стартовали в забеге на 100 м. Когда Саша финишировал, Лёша находился в десяти метрах позади него, а когда финишировал Лёша — Коля находился позади него в десяти метрах. На каком расстоянии друг от друга находились Саша и Коля, когда Саша финишировал? (Предполагается, что все мальчики бегут с постоянными, но, конечно, не равными скоростями.)

В музее 16 залов, расположенных как показано на рисунке.

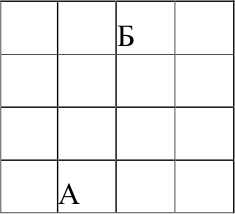
В половине из них выставлены картины, а в половине скульптуры. Из любого зала можно попасть в любой соседний с ним (имеющий общую стену). При любом осмотре музея залы чередуются: зал с картинами — зал со скульптурами — зал с картинами и т.д. Осмотр начинается в зале А, в котором висят картины, а заканчивается в зале Б.

1. Обозначьте крестиками все залы, в которых висят картины.
2. Турист хочет осмотреть как можно больше залов (пройти от зала А к залу Б), но при этом в каждом зале побывать не больше одного раза. Какое наибольшее количество залов он сможет посмотреть? Нарисуйте какой-нибудь его маршрут наибольшей длины и докажите, что большее количество залов он посмотреть не мог.