Всероссийская олимпиада школьников по математике, 10 класс, 2014 год
дата проведения: 22 сентября 2014 - 29 сентября 2014
Задача 4.
В квадрате со стороной 5 произвольным образом отметили 201 точку. Верно ли, что какие-то 5 точек можно накрыть квадратом со стороной 1?
Ответ на Задачу 4.
Ответ: Да.
Решение:
Разделим данный квадрат со стороной 5 прямыми, параллельными его сторонам, на 25 квадратов со стороной 1 (см. рисунок).
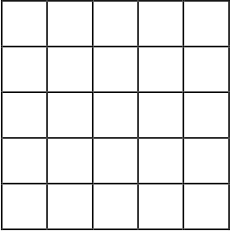
Если бы в каждом таком квадрате было не больше 4 отмеченных точек, то всего было бы отмечено не более 25 ⋅ 4 = 100 точек, что противоречит условию. Следовательно, хотя бы в одном из полученных квадратов должно быть 5 из отмеченных точек.

