Задача 5.
На числовой прямой закрашивают красным и синим цветом точки с целыми координатами по следующим правилам:
- точки, разность координат которых равна 7, должны быть покрашены одним цветом;
- точки с координатами 20 и 14 должны быть покрашены красным, а точки с координатами 71 и 143 — синим.
Сколькими способами можно раскрасить все целые числа, соблюдая эти правила?
Ответ на Задачу 5.
Ответ: 8 способами.
Решение:
Из пункта а) следует, что раскраска всех точек с целыми координатами однозначно определяется раскраской точек, соответствующих числам 0, 1, 2, 3, 4, 5 и 6. Точка 0 = 14 − 2⋅7 должна быть покрашена так же как 14, т.е. красным. Аналогично, точка 1 = 71 − 10⋅7 должна быть покрашена синим, точка 3 = 143 − 20⋅7 — синим, и 6 = 20 − 2⋅7 — красным. Поэтому остаётся только посчитать, сколькими различными способами можно раскрасить точки, соответствующие числам 2, 4 и 5. Так как каждую точку можно раскрасить двумя способами — красным или синим — то всего способов 2⋅2⋅2 = 8.
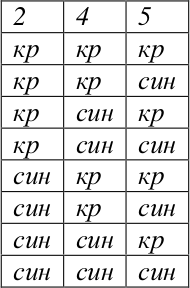
Примечание: При подсчёте числа способов раскрашивания точек 2, 4 и 5, можно просто перечислить все способы, например, в виде таблицы: