Ответ: В 4 раза.

Решение:

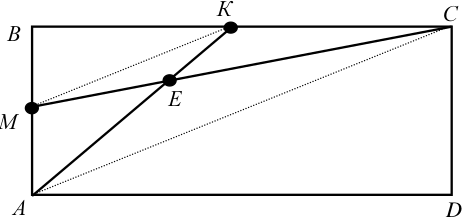
Проведем отрезки $MK$ и $AC$. Четырёхугольник $MBKE$ состоит из треугольников $MBK$ и $MKE$, а четырёхугольник $AECD$ — из треугольников $AEC$ и $ACD$. Далее можно рассуждать разными способами.

1 способ.

Треугольники $MBK$ и $ACD$ — прямоугольные и катеты первого в 2 раза меньше катетов второго, поэтому они подобны и площадь треугольника $ACD$ в 4 раза больше площади треугольника $MBK$.

Т.к. $M$ и $K$ — середины $AB$ и $BC$ соответственно, то $MK$ — средняя линия треугольника $ABC$, поэтому $MK$ || $AC$ и $MK$ = 0,5$AC$. Из параллельности прямых $MK$ и $AC$ следует подобие треугольников $MKE$ и $AEC$, а т.к. коэффициент подобия равен 0,5, то площадь треугольника $AEC$ в 4 раза больше площади треугольника $MKE$.

Теперь:

$S_{AECD}$ = $S_{AEC} + S_{ACD}$ = $4S_{MKE} + 4S_{MBK}$ = $4(S_{MKE} + S_{MBK})$ = $4S_{MBKE}$

2 способ.

Пусть площадь прямоугольника $ABCD$ равна $S$. Тогда площадь треугольника $ACD$ равна $\displaystyle \frac{1}{2}S$ (диагональ прямоугольника делит его на два равных треугольника), а площадь треугольника $MBK$ равна:

$\displaystyle \frac{1}{2}MB⋅BK$ = $\displaystyle \frac{1}{2}⋅\frac{1}{2}AB⋅\frac{1}{2}BC$ = $\displaystyle \frac{1}{8}AB⋅BC$ = $\displaystyle \frac{1}{8}S$.

Т.к. $M$ и $K$ — середины отрезков $AB$ и $BC$, то $AK$ и $CM$ — медианы треугольника $ABC$, поэтому $E$ — точка пересечения медиан треугольника $ABC$, т.е. расстояние от $E$ до $AC$ равно $\displaystyle \frac{1}{3}h$, где $h$ — высота треугольника $ABC$, проведённая из вершины $B$. Тогда площадь треугольника $AEC$ равна:

$\displaystyle \frac{1}{2}AC⋅\left(\frac{1}{3}h\right)$ = $\displaystyle \frac{1}{3}⋅\left(\frac{1}{2}AC⋅h\right)$ = $\displaystyle \frac{1}{3}S_{ABC}$ = $\displaystyle \frac{1}{3}⋅\left(\frac{1}{2}S\right)$ = $\displaystyle \frac{1}{6}S$

Тогда для площади четырёхугольника $AECD$, равной сумме площадей треугольников $AEC$ и $ACD$, получаем:

$\displaystyle \frac{1}{2}S + \frac{1}{6}S$ = $\displaystyle \frac{2}{3}S$

Далее, т.к. $MK$ – средняя линия треугольника $ABC$, то площадь треугольника $MKE$ равна:

$\displaystyle \frac{1}{2}MK⋅\left(\frac{1}{2}h − \frac{1}{3}h\right)$ = $\displaystyle \frac{1}{2}\left(\frac{1}{2}AC\right)⋅\left(\frac{1}{6}h\right)$ = $\displaystyle \frac{1}{12}\left(\frac{1}{2}AC⋅h\right)$ = $\displaystyle \frac{1}{12}S_{ACD} = \frac{1}{24}S$

Поэтому для площади четырёхугольника $MBKE$, равной сумме площадей треугольников $MBK$ и $MKE$, получаем:

$\displaystyle \frac{1}{8}S + \frac{1}{24}S$ = $\displaystyle \frac{1}{6}S$

Таким образом, отношение площадей четырёхугольников $AECD$ и $MBKE$ равно:

$\displaystyle \frac{2}{3}S:\left(\frac{1}{6}S\right)$ = 4.