Ответ: Один из возможных примеров приведён на рисунке:

Решение 1:

Если группировать прямоугольники: первый с последним, второй с предпоследним и т.д., то получаются одинаковые полоски длины 14: 1 + 13 = 14, 2 + 12 = 14, 3 + 11 = 14, … Из нескольких одинаковых полосок легко сложить прямоугольник, прикладывая их друг к другу длинной стороной. Однако, если мы попробуем продолжить описанный выше процесс, возникнет проблема: центральная полоска 7×1 останется без пары. Проблему можно решить так: самую длинную полоску длины 13 оставить одну, а оставшиеся сгруппировать по тому же принципу (самую короткую с самой длинной и т.д.): 13, 1 + 12, 2 + 11, 3 + 10, 4 + 9, 5 + 8, 6 + 7. Приложив получившиеся полоски длины 13 друг к другу, получаем пример, приведённый выше.

Решение 2:

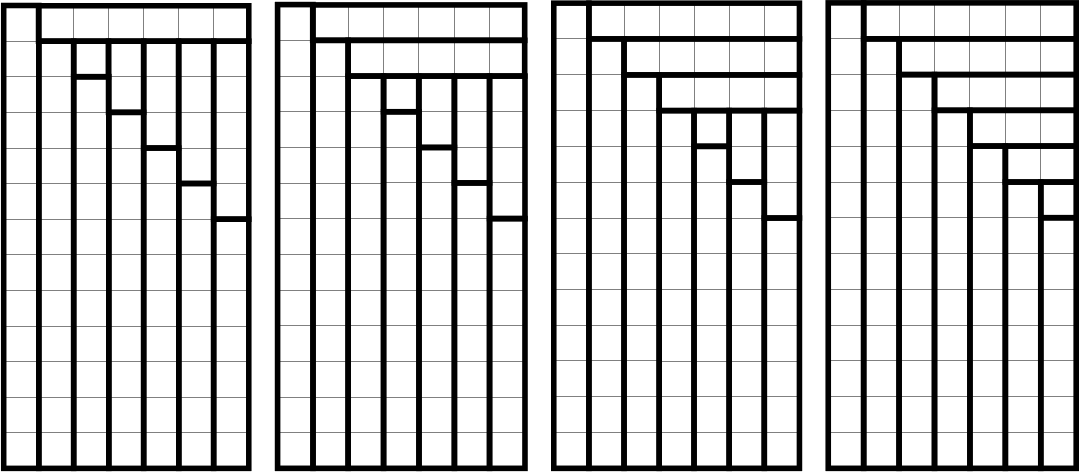
Площадь итогового прямоугольника равна 1 + 2 + 3 + 4 + … + 13 = 91. Т.к. в разложении 91 на простые множители всего два множителя: 91 = 7·13, то стороны итогового прямоугольника однозначно определяются – они должны быть 7 и 13. Прямоугольника других размеров (так, чтобы его стороны были больше 1) сложить из данных прямоугольничков нельзя. При этом внутри итогового прямоугольника исходные прямоугольнички могут размещаться по-разному. Некоторые варианты расположения приведены ниже: