Задача 5.
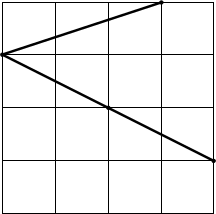
На стандартном тетрадном листе в клетку нарисован угол (см. рисунок). Найдите его величину, не используя измерительные инструменты. Ответ обоснуйте.
Ответ на Задачу 5.
Ответ: 45°.
Решение:
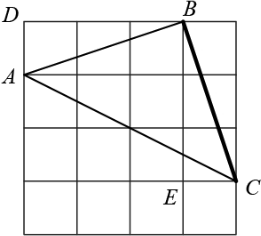
Соединим две «крайние» точки отрезком (как на рисунке). Получившийся треугольник — равнобедренный, так как две его стороны $AB$ и $BC$ являются диагоналями трёхклеточных прямоугольников. Диагональ $AB$ делит угол прямоугольника с вершиной $B$ на два угла, дополняющих друг друга до прямого. Треугольники $ADB$ и $CEB$ равны по двум катетам, значит, равны их соответствующие углы. И значит, угол $CBE$ дополняет угол $ABE$ до прямого. Таким образом, треугольник $ABC$ — равнобедренный и прямоугольный. Его углы $A$ и $C$ при основании $AC$ равны по свойству равнобедренного треугольника и имеют величину 45° по теореме о сумме углов треугольника.

