Задача 1.
Подберите такие не равные нулю числа $n$ и $m$, чтобы равенство $(n ⋅ 5^n)^n = m ⋅ 5^9$ было верным.
Задача 2.
В подводном царстве живут осьминоги с семью и восемью ногами. Те, у кого 7 ног, всегда врут, а те, у кого 8 ног, всегда говорят правду. Однажды между трёмя осьминогами состоялся такой разговор.
- Зелёный осьминог: «У нас вместе 24 ноги».
- Синий осьминог: «Ты прав!»
- Красный осьминог: «Глупости, Зелёный говорит ерунду!»
Сколько ног было у каждого осьминога? (Ответ обоснуйте.)
Задача 3.
Фирма изготавливает лимонный напиток, разбавляя лимонный сок водой. Сначала фирма производила напиток, содержащий 15% лимонного сока. Через некоторое время генеральный директор отдал указание снизить содержание лимонного сока до 10%. На сколько процентов увеличится количество производимого лимонного напитка при тех же объёмах поставок лимонов?
Задача 4.
Все натуральные числа, сумма цифр в записи которых делится на 5, выписывают в порядке возрастания: 5, 14, 19, 23, 28, 32, … Чему равна самая маленькая положительная разность между соседними числами в этом ряду? Приведите пример и объясните, почему меньше быть не может.
Задача 5.
На стандартном тетрадном листе в клетку нарисован угол (см. рисунок). Найдите его величину, не используя измерительные инструменты. Ответ обоснуйте.
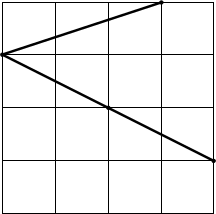
Задача 6.
На координатной плоскости есть точки, координаты ($x$; $y$) которых удовлетворяют уравнению:
$y(x + 1) = x^2 − 1$
Например, одна из них — точка с координатами (1;0). Изобразите все точки, координаты ($x$; $y$) которых удовлетворяют этому уравнению.

