Всероссийская олимпиада школьников по математике, 8 класс, 2014 год, 2 этап
дата проведения: 22 сентября 2014 - 29 сентября 2014
Задача 6.
На координатной плоскости есть точки, координаты ($x$; $y$) которых удовлетворяют уравнению:
$y(x + 1) = x^2 − 1$
Например, одна из них — точка с координатами (1;0). Изобразите все точки, координаты ($x$; $y$) которых удовлетворяют этому уравнению.
Ответ на Задачу 6.
Ответ: См. рисунок.
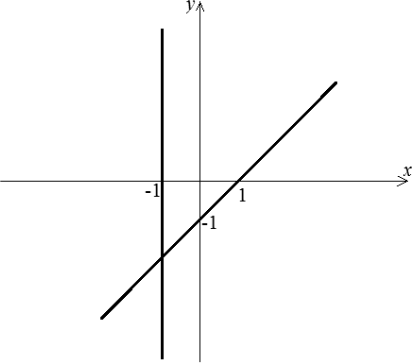
Решение:
Преобразуем уравнение следующим образом:
$y(x + 1) = (x − 1)(x + 1)$
$y(x + 1) − (x − 1)(x + 1) = 0$
$(x + 1)(y − x + 1) = 0$
Отсюда $x$ = −1 или $y$ = $x$ − 1. Таким образом, все точки с координатами, удовлетворяющими уравнению, представляют собой совокупность двух прямых: прямой, параллельной оси ординат и проходящей через точку (−1;0) и прямой, являющейся графиком функции $y$ = $x$ − 1 (см. рисунок).

