Всероссийская олимпиада школьников по математике, 9 класс, 2014 год
дата проведения: 22 сентября 2014 - 29 сентября 2014
Задача 5.
В окружности провели диаметр $AB$ и параллельную ему хорду $CD$ так, что расстояние между ними равно половине радиуса этой окружности (см. рисунок). Найдите угол $CAB$.
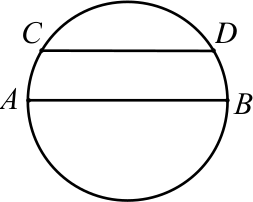
Ответ на Задачу 5.
Ответ: 75°.
Решение:
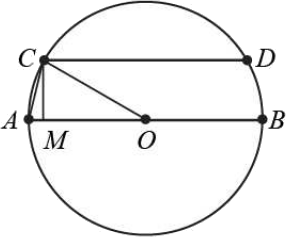
Рассмотрим треугольник $AOC$, где $O$ — центр окружности. Этот треугольник равнобедренный, так как $OC$ и $OA$ — радиусы. Значит, по свойству равнобедренного треугольника, углы $A$ и $C$ равны. Проведем перпендикуляр $CM$ к стороне $AO$ и рассмотрим прямоугольный треугольник $OMC$. По условию задачи, катет $CM$ — половина гипотенузы $OC$. Значит, величина угла $COM$ равна 30°. Тогда, по теореме о сумме углов треугольника получаем, что угол $CAO$ (или $CAB$) равен 75°.

