Задача 1.
Отмечено 9 точек, как показано на рисунке. Нарисуйте два различных по форме семиугольника с вершинами в отмеченных точках. Для каждого семиугольника сделайте отдельный чертёж.

Задача 2.
В тот день, когда Диму поздравляли с днём рождения его брат и сестра, Дима сказал: «Смотрите, как интересно, я теперь вдвое старше брата и втрое старше сестры!» «А ваш средний возраст 11 лет», — подхватил папа. Сколько лет исполнилось Диме?
Задача 3.
Однажды следователю пришлось допрашивать трёх свидетелей ограбления: Джона Уайта, Сэма Грэя и Боба Блэка. Джон уверял, что все показания Сэма — сплошная ложь, а Сэм только и делал, что твердил, будто Боб говорит неправду. Боб же всё это время уговаривал следователя не верить ни Уайту, ни, тем более, Грэю. Следователь, будучи человеком сообразительным и умным, попросил всех троих замолчать и, не задав более ни одного вопроса, быстро определил, с кем из них стоит иметь дело, а с кем — нет. Кто же из свидетелей не лгал?
Задача 4.
Сколько существует трёхзначных чисел, которые в 5 раз больше произведения своих цифр?
Задача 5.
В окружности провели диаметр $AB$ и параллельную ему хорду $CD$ так, что расстояние между ними равно половине радиуса этой окружности (см. рисунок). Найдите угол $CAB$.
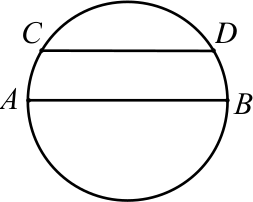
Задача 6.
Постройте график уравнения $x^2 − y^4 = \sqrt{18x − x^2 − 81}$, то есть изобразите на координатной плоскости все точки, координаты $(x;y)$ которых удовлетворяют этому уравнению.

