Всероссийская олимпиада школьников по математике, 9 класс, 2014 год
дата проведения: 22 сентября 2014 - 29 сентября 2014
Задача 6.
Постройте график уравнения $x^2 − y^4 = \sqrt{18x − x^2 − 81}$, то есть изобразите на координатной плоскости все точки, координаты $(x;y)$ которых удовлетворяют этому уравнению.
Ответ на Задачу 6.
Ответ: См. рисунок.
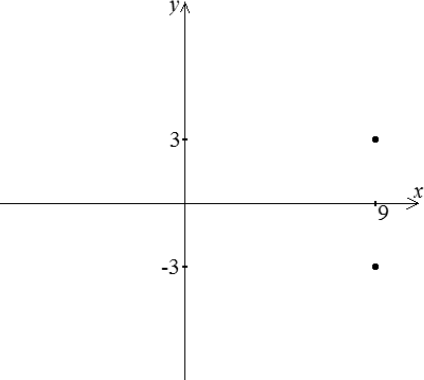
Решение:
Преобразуем данное уравнение, выделив под знаком корня полный квадрат:
$x^2 − y^4 = \sqrt{−(x − 9 )^2}$
Выражение в правой части имеет смысл лишь при $x = 9$. Подставляя это значение в уравнение, получаем:
$9^2 - y^4 = 0$
Разложим на множители левую часть:
$(3 - y)(3 + y)(9 + y^2) = 0$
Откуда $y = 3$ или $y = -3$. Значит, координаты только двух точек (9; 3) или (9; −3) удовлетворяют данному уравнению. График уравнения изображён на рисунке выше.

