Задача 1.
В таблице 3 × 3 записаны числа, как показано на рисунке. За ход разрешается выбрать три клетки в форме трёхклеточного уголка и уменьшить число в каждой из них на 1. Покажите, как такими операциями сделать таблицу, в которой во всех клетках стоят нули.
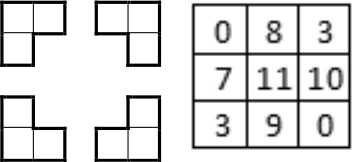
Ответ на Задачу 1.
Решение:
Один из способов таков:

Сначала обнуляем угловые ячейки с числами «3» вместе с их соседями. Затем уменьшаем ячейки с числами 4, 11 и 5. Потом уменьшаем ячейки с числами 6, 7, 7. Из результата легко получается таблица с нулями.
Примечание: Заметим, что сумма чисел на большой диагонали равна 17, а сумма остальных чисел равна 34. Поэтому если выбирать только уголки, в которых одна клетка лежит на диагонали, а две другие нет, то при каждом шаге сумма чисел на диагонали будет уменьшаться на 1, а сумма остальных чисел на 2. Остаётся показать правильную последовательность выбора таких уголков.

