Задача 1.
В таблице 3 × 3 записаны числа, как показано на рисунке. За ход разрешается выбрать три клетки в форме трёхклеточного уголка и уменьшить число в каждой из них на 1. Покажите, как такими операциями сделать таблицу, в которой во всех клетках стоят нули.
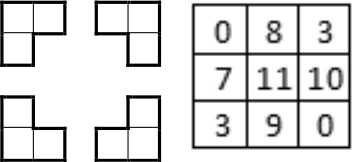
Задача 2.
Делится ли 132013 + 132014 + 132015 на 61?
Задача 3.
Даны два уравнения $ax^2 + bx + c = 0$ и $cx^2 + bx + a = 0$, в которых все коэффициенты ненулевые. Оказалось, что они имеют общий корень. Верно ли, что $a = c$?
Задача 4.
В некоторой школе каждый десятиклассник либо всегда говорит правду, либо всегда лжёт. Директор вызвал к себе нескольких десятиклассников и спросил каждого из них про каждого из остальных, правдивец тот или лжец. Всего было получено 44 ответа «правдивец» и 28 ответов «лжец». Сколько правдивых ответов мог получить директор?
Задача 5.
Могут ли две биссектрисы треугольника разбивать его на четыре части равной площади?
Задача 6.
Существует ли натуральное число, кратное 2015, сумма цифр которого равна 2015?

