Ответ: Нет, не могут.

Решение:

Способ 1.

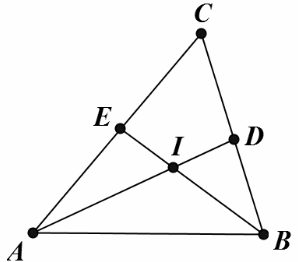
Пусть такое возможно, т.е. биссектрисы $AD$ и $BE$ треугольника $ABC$ разбивают его на четыре части равной площади. Пусть $I$ точка — пересечения указанных биссектрис. Равновеликие треугольники $AIB$ и $AIE$ имеют общую высоту, проведённую из вершины $A$, поэтому $BI$ = $IE$. Аналогично, из равенства площадей треугольников $AIB$ и $DIB$ следует равенство $AI$ = $ID$. Значит, диагонали четырёхугольника $AEDB$ точкой пересечения делятся пополам, т.е. $AEDB$ — параллелограмм. Это невозможно, так как прямые $AE$ и $BD$ не параллельны, они пересекаются в точке $C$.

Способ 2.

Пусть такое возможно, т.е. биссектрисы $AD$ и $BE$ треугольника $ABC$ разбивают его на четыре части равной площади. Треугольники $ACD$ и $ABD$ равновелики, поэтому биссектриса $AD$ — медиана. Аналогично $BE$ — медиана. Три медианы делят треугольник на шесть равновеликих частей, значит, площадь треугольника $AIE$ составляет шестую часть площади треугольника $ABC$, а не четверть (как в условии). Противоречие.

Примечание: Заметим, что из решения первым способом следует, что условие задачи избыточно, достаточно равенства площадей трёх получившихся треугольников.