Задача 5.
Прямоугольник $ABCD$ разделили на четыре меньших прямоугольника с одинаковыми периметрами (см. рисунок). Известно, что $AB$ = 18 см, а $BC$ = 16 см. Найдите длины сторон остальных прямоугольников. Обязательно объясните свой ответ.
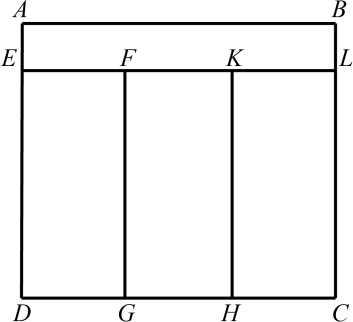
Ответ на Задачу 5.
Ответ: 2 см и 18 см — длины сторон прямоугольника $ABLE$, 6 см и 14 см — длины сторон остальных прямоугольников.
Решение:
Так как периметры трёх вертикальных прямоугольников равны и к тому же равны отрезки $ED$, $FG$, $KH$ и $LC$, отрезки $EF$, $FK$ и $KL$ тоже равны. Значит, каждый из отрезков $EF$, $FK$ и $KL$ равен 18 см : 3 = 6 см.
Периметр прямоугольника $ABLE$ равен периметру прямоугольника $DEFG$. Дальше можно решать, составив уравнение, или попытаться обойтись без него.
Способ 1.
Пусть $AE$ = $x$ см, тогда 18 + 18 + $x$ + $x$ = 6 + 6 + 16 − $x$ + 16 − $x$. Откуда находим $x$ = 2 . Значит, $AE$ = 2 см, а $ED$ = 14 см.
Способ 2.
Из условия следует, что $DE$ + $EF$ = $AE$ + $AB$, то есть $DE$ + 6 = $AE$ + 18. Тогда разность длины отрезков $DE$ и $AE$ равна 12 см, а их сумма по условию равна 16 см. Отсюда $AE$ = 2 см, а $DE$ = 14 см.

