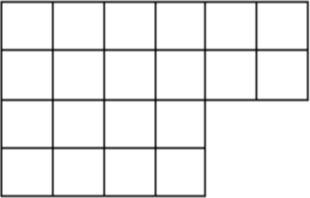
Задача 1.
У Пети есть картонная фигура, показанная на рисунке. Как ему разрезать эту фигуру по линиям клеток на четыре равные фигуры (то есть такие фигуры, из которых любые две можно наложить друг на друга так, чтобы они совпали)?
Задача 2.
Число 11 можно представить в виде суммы четырёх квадратов чисел только одним способом, не считая порядка слагаемых:
11 = 9 + 1 + 1 + 0 = 32 + 12 + 12 + 02
Можно ли число 99 представить в виде суммы четырёх квадратов двумя различными способами?
Задача 3.
Шестнадцать мальчишек собрались на рыбалку. Известно, что каждый мальчишка, который надел сапоги, надел и кепку. Без сапог оказалось 10 мальчишек, а без кепки — двое. Каких мальчишек и на сколько больше: тех, кто был в кепке, но без сапог, или тех, кто надел сапоги? Обязательно объясните свой ответ.
Задача 4.
Саша поехал в гости к бабушке. В субботу он сел в поезд, а через 50 часов в понедельник доехал до бабушкиного города. Саша заметил, что в этот понедельник число совпало с номером вагона, в котором он ехал, что номер его места в вагоне был меньше номера вагона и что в ту субботу, когда он садился в поезд, число было больше номера вагона. Какими были номера вагона и места? Обязательно объясните свой ответ.
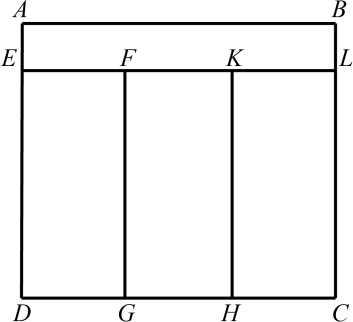
Задача 5.
Прямоугольник $ABCD$ разделили на четыре меньших прямоугольника с одинаковыми периметрами (см. рисунок). Известно, что $AB$ = 18 см, а $BC$ = 16 см. Найдите длины сторон остальных прямоугольников. Обязательно объясните свой ответ.