Всероссийская олимпиада школьников по математике, 10 класс, 2016 год
дата проведения: 10 октября 2016 - 16 октября 2016
Задача 4.
На координатной плоскости изображены графики функций $y$ = $x^2$ + $bx$ + $c$ и $y$ = $x^2$ + $cx$ + $b$. Найдите значения $b$ и $c$. В ответе запишите уравнения каждой из функций.
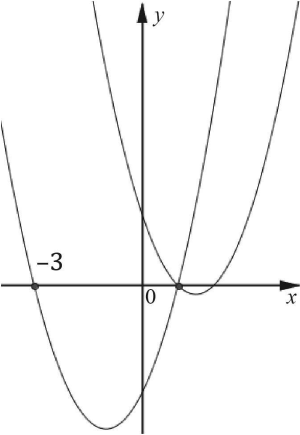
Ответ на Задачу 4.
Ответ: $y$ = $x^2$+ 2$x$ − 3 и $y$ = $x^2$ − 3$x$ + 2.
Решение:
Некоторое число $t$ является корнем обоих трёхчленов, поэтому $t^2$ + $bt$ + $c$ = $t^2$ + $ct$ + $b$, откуда ($b$ − $c$)($t$ − 1) = 0. Так как $b$ ≠ $c$ (иначе параболы совпадут), получаем, что $t$ = 1. Если парабола $y$ = $x^2$ + $bx$ + $c$ пересекает ось абсцисс в точках −3 и 1, то по теореме, обратной теореме Виета $b$ = −(−3 + 1) = 2, $c$ = −3 ⋅ 1 = −3.

