Задача 1.
Точка $O$ — центр квадрата $ABCD$. Найдите какие-нибудь семь попарно неравных векторов с концами и началами в точках $A$, $B$, $C$, $D$, $O$, сумма которых равна нулевому вектору. Объясните свой ответ.
Задача 2.
Можно ли все натуральные числа от 1 до 800 разбить на пары так, чтобы сумма любой пары чисел делилась на 6?
Задача 3.
Участвуя в шахматном турнире, Вася сыграл 52 партии. По 1 старой системе подсчёта очков (1 очко за победу, ½ очка за ничью и 0 очков за поражение) он набрал 35 очков. Сколько очков он набрал по новой системе подсчёта очков (1 очко за победу, 0 очков за ничью и −1 очко за поражение)?
Задача 4.
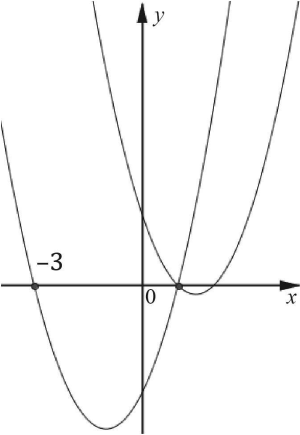
На координатной плоскости изображены графики функций $y$ = $x^2$ + $bx$ + $c$ и $y$ = $x^2$ + $cx$ + $b$. Найдите значения $b$ и $c$. В ответе запишите уравнения каждой из функций.
Задача 5.
Две вершины, центр вписанной окружности и точка пересечения высот остроугольного треугольника лежат на одной окружности. Найдите угол при третьей вершине.
Задача 6.
Петя показал Васе 37 внешне одинаковых карточек, выложенных в ряд. Он сказал, что на закрытых сторонах карточек записаны все числа от 1 до 37 (каждое по одному разу) так, что число на любой карточке начиная со второй является делителем суммы чисел, написанных на всех предшествующих карточках. Затем Петя показал Васе, что на первой карточке написано число 37, а на второй — число 1. Вася сказал, что он тогда знает, какое число написано на третьей карточке. Какое?

