Ответ: 60°.

Решение:

Рассмотрим треугольник $ABC$, в котором проведены высоты $AA_1$ и $BB_1$. Пусть точка $H$ — точка пересечения высот, точка $I$ — центр вписанной окружности.

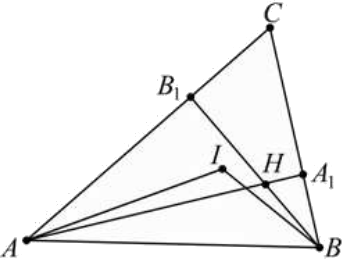
1. Сумма углов четырёхугольника $A_1HB_1C$ равна 360°. Получаем:

$∠AHB$ = $∠A_1HB_1$ = 360° − 90° − 90° − $∠C$ = 180° − $∠C$

2. По теореме о сумме углов треугольника имеем соотношения $∠A$ + $∠B$ + $∠C$ = 180° (для треугольника $ABC$) и $\displaystyle \frac{∠A}{2} + \frac{∠B}{2}$ + $∠AIB$ = 180° (для треугольника $ABI$). Отсюда:

$∠AIB$ = 180° − $\displaystyle \frac{∠A + ∠B}{2}$ = 180° − (180° − $∠C$) : 2 $\quad \Rightarrow \quad ∠AIB$ = 90° + $\displaystyle \frac{∠C}{2}$

3. Точки $A$, $B$, $H$ и $I$ лежат на одной окружности. Так как треугольник $ABC$ остроугольный, точки $H$ и $I$ лежат по одну сторону от хорды $AB$, то есть вписанные углы $AIB$ и $AHB$ опираются на одну и ту же дугу. Значит,

$∠AIB$ = $∠AHB$, откуда

90° + $\displaystyle \frac{∠C}{2}$ = 180° − $∠C$, а значит $∠C$ = 60°.