Задача 3.
Дима начертил графики четырёх линейных функций на координатной плоскости, но забыл отметить единичные отрезки. Когда он переписывал задание в тетрадь, то отвлекся и не дописал уравнения, задающие функции под номерами 3 и 4. Найдите эти уравнения. Ответ обоснуйте.
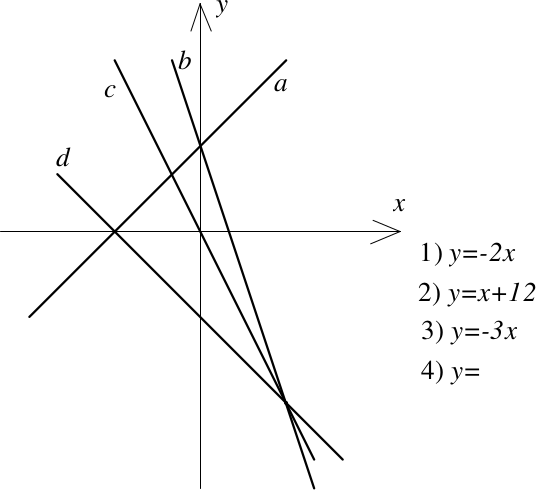
Ответ на Задачу 3.
Ответ: 3) $y$ = −3$x$ + 12; 4) $y$ = −$x$ − 12.
Решение:
Из четырёх прямых только прямая $a$ имеет положительный угловой коэффициент, следовательно, она задаётся уравнением 2 и пересекает оси координат в точках (0; 12) и (−12; 0).
Так как уравнение 1 Дима записал полностью, его графиком является прямая, проходящая через начало координат, то есть прямая $c$.
У прямой $b$ модуль углового коэффициента больше, чем у прямой $c$, значит, начало уравнения прямой $b$ Дима записал под номером 3. Так как эта прямая проходит через точку (0; 12), она задаётся уравнением $y$ = −3$x$ + 12.
Прямая $d$ проходит через точку (−12; 0) и через точку (12; −24) — точку пересечения прямых $b$ и $c$, координаты которой легко находятся как решение системы линейных уравнений: $y$ = −3$x$ + 12 и $y$ = −2$x$.
Найдём уравнение прямой $d$. Для этого рассмотрим систему двух уравнений:
0 = −12$k_4$ + $b_4$
−24 = 12$k_4$ + $b_4$
Сложив эти уравнения, получим $b_4$ = −12. Подставив в первое уравнение, получим $k_4$ = −1.

