В равенстве 1 − 2 − 4 − 8 − 16 = 19 поставьте несколько знаков модуля так, чтобы оно стало верным.

Чебурашка и Гена съели торт. Чебурашка ел вдвое медленнее Гены, но начал есть на минуту раньше. В итоге им досталось торта поровну. За какое время Чебурашка съел бы торт в одиночку?

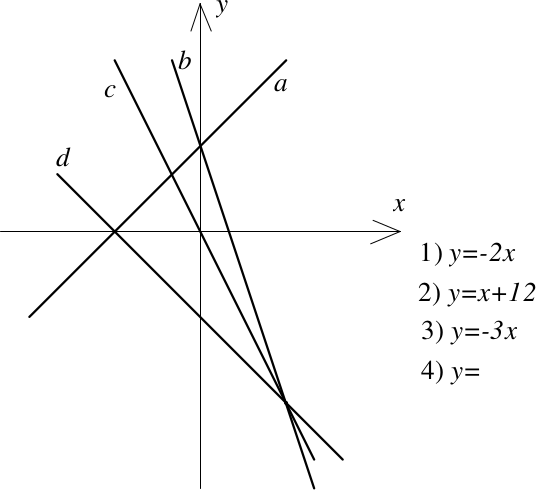
Дима начертил графики четырёх линейных функций на координатной плоскости, но забыл отметить единичные отрезки. Когда он переписывал задание в тетрадь, то отвлекся и не дописал уравнения, задающие функции под номерами 3 и 4. Найдите эти уравнения. Ответ обоснуйте.

Три школьника сделали по два утверждения про натуральные числа $a$, $b$, $c$:

• Антон: 1) $a$ + $b$ + $c$ = 34; 2) $abc$ = 56;
• Борис: 1) $ab$ + $bc$ + $ac$ = 311 2) наименьшее из чисел равно 5;
• Настя: 1) $a$ = $b$ = $c$ 2) числа $a$, $b$ и $c$ — простые.

У каждого школьника одно утверждение верное, а другое — нет. Найдите числа $a$, $b$, $c$.

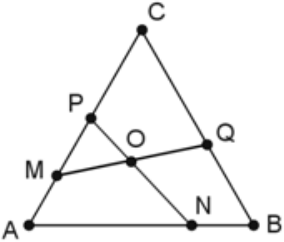
В равностороннем треугольнике $ABC$ со стороной $a$ точки $M$, $N$, $P$, $Q$ расположены так, как показано на рисунке. Известно, что $MA$ + $AN$ = $PC$ + $CQ$ = $a$. Найдите величину угла $NOQ$.

На шахматной доске стоял 21 король. Каждый из королей находился под боем хотя бы одного из остальных. После того как несколько королей убрали, никакие два из оставшихся королей друг друга не бьют. Какое наибольшее число королей могло остаться?

1. Приведите пример исходной расстановки и отметьте убранных королей.
2. Докажите, что большее число королей остаться не могло.