Всероссийская олимпиада школьников по математике, 9 класс, 2016 год
дата проведения: 10 октября 2016 - 16 октября 2016
Задача 5.
В равностороннем треугольнике $ABC$ со стороной $a$ точки $M$, $N$, $P$, $Q$ расположены так, как показано на рисунке. Известно, что $MA$ + $AN$ = $PC$ + $CQ$ = $a$. Найдите величину угла $NOQ$.
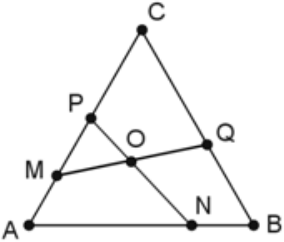
Ответ на Задачу 5.
Ответ: 60°
Решение:
По условию задачи $AN$ = $a$ – $AM$, следовательно, $AN$ = $MC$. Аналогично $AP$ = $QC$. Из этих равенств и равенства $∠A$ = $∠C$ = 60° следует, что $∆ANP$ = ∆$CMQ$. Отсюда $∠ANP$ = $∠QMC$, $∠APN$ = $∠MQC$.
По теореме о сумме углов треугольника $∠ANP$ + $∠APN$ = 120°, поэтому $∠OMP$ + $∠OPM$ = 120°, а значит, $∠MOP$ = 60°. Углы $MOP$ и $NOQ$ вертикальные, поэтому $∠NOQ$ = 60°.

