Всероссийская олимпиада школьников по математике, 10 класс, 2017 год
дата проведения: 16 октября 2017 - 22 октября 2017
Задача 4.
Сравните величины углов $BAC$ и $CED$ (см. рисунок). Свой ответ обоснуйте.
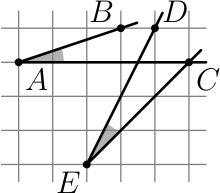
Ответ на Задачу 4.
Ответ: эти углы равны.
Решение:
Пусть $K$ — основание перпендикуляра, опущенного из $B$ на $AC$.
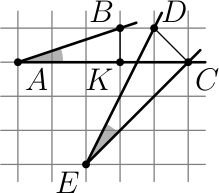
Рассмотрим треугольники $ABK$ и $EDC$. Они оба прямоугольные, причём их катеты относятся как 1 : 3. Значит, тангенсы отмеченных углов равны 1/3, то есть сами углы тоже равны.

