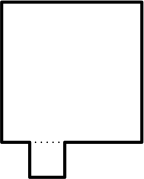
Замок Персиваля имел квадратную форму. Однажды Персиваль решил расширить свои владения и добавил к замку квадратную пристройку. В результате периметр замка увеличился на 10%. На сколько процентов увеличилась площадь замка?

Известно, что $a^2 + b = b^2 + c = c^2 + a$. Какие значения может принимать выражение:

$a\left(a^2 − b^2\right) + b\left(b^2 − c^2\right) + c\left(c^2 − a^2\right)$

На доске в произвольном порядке выписаны числа от 1 до 2017. Два числа можно поменять местами, если одно из них делится на другое. Докажите, что за несколько таких операций числа можно расположить в порядке возрастания.

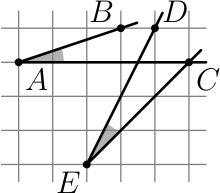
Сравните величины углов $BAC$ и $CED$ (см. рисунок). Свой ответ обоснуйте.

Лёша не поленился вычислить сумму:

$9 + 99 + 999 + \ldots + \underbrace{9\ldots9}_{2017}$

и выписать её на доску. Сколько раз в итоговом результате записана цифра 1?

Несколько мудрецов построилось в колонну. На всех были либо чёрные, либо белые колпаки. Оказалось, что среди любых 10 подряд идущих мудрецов поровну мудрецов с белыми и с чёрными колпаками, а среди любых 12 подряд идущих — не поровну. Какое наибольшее количество мудрецов могло быть?