Всероссийская олимпиада школьников по математике, 8 класс, 2017 год, 2 этап
дата проведения: 16 октября 2017 - 22 октября 2017
Задача 2.
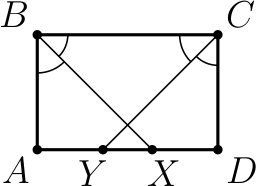
В прямоугольнике $ABCD$ сторона $AB$ равна 6, сторона $BC$ равна 11. Из вершин $B$ и $C$ проведены биссектрисы углов, пересекающие сторону $AD$ в точках $X$ и $Y$ соответственно. Найдите длину отрезка $XY$.
Ответ на Задачу 2.
Ответ: 1.
Решение:
Углы $AXB$ и $XBC$ равны как накрест лежащие при параллельных прямых $AD$ и $BC$ и секущей $BX$. Углы $XBC$ и $XBA$ равны, так как $BX$ — биссектриса угла $ABC$. Получаем, что $∠AXB$ = $∠XBA$, откуда следует, что треугольник $AXB$ — равнобедренный, $AB$ = $AX$ = 6; $XD$ = $AD$ − $AX$ = 11 − 6 = 5. Аналогично получаем, что $AY$ = 5. Тогда $XY$ = $AD$ − $AY$ − $XD$ = 11 − 5 − 5 = 1.

