Представьте число 2017 в виде суммы пяти натуральных чисел так, чтобы все цифры, использованные в этих пяти числах, были различны.

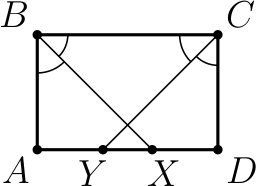
В прямоугольнике $ABCD$ сторона $AB$ равна 6, сторона $BC$ равна 11. Из вершин $B$ и $C$ проведены биссектрисы углов, пересекающие сторону $AD$ в точках $X$ и $Y$ соответственно. Найдите длину отрезка $XY$.

Рыцарский турнир длится ровно 7 дней. К концу четвёртого дня сэр Ланселот не успел сразиться лишь с одной четвертью от общего числа участников турнира. А сэр Тристан к этому времени сразился ровно с одной седьмой из тех рыцарей, с кем успел сразиться сэр Ланселот. Какое минимальное количество рыцарей могло участвовать в турнире?

Володя расставил несколько (возможно 0) шахматных фигур на доску 8 × 8. Лёня заметил, что в каждом квадрате 2 × 2 стоит одинаковое количество фигур. А Влад заметил, что в каждом прямоугольнике 3 × 1 (или 1 × 3) стоит одинаковое количество фигур. Сколько фигур было выставлено на доску? (Укажите все варианты и докажите, что других нет)

Три школьницы зашли в магазин. Аня купила 2 ручки, 7 карандашей и 1 блокнот, Варя — 5 ручек, 6 карандашей и 5 блокнотов, Саша — 8 ручек, 4 карандаша и 9 блокнота. Все заплатили поровну, но одна при оплате воспользовалась скидкой. Кто? (Объясните свой ответ).

В треугольнике $ABC$ провели медиану $AM$. Найдите угол $AMC$, если углы $BAC$ и $BCA$ равны 45° и 30° соответственно.