Всероссийская олимпиада школьников по математике, 8 класс, 2017 год, 2 этап
дата проведения: 16 октября 2017 - 22 октября 2017
Задача 6.
В треугольнике $ABC$ провели медиану $AM$. Найдите угол $AMC$, если углы $BAC$ и $BCA$ равны 45° и 30° соответственно.
Ответ на Задачу 6.
Ответ: 135°.
Решение:
Пусть $BH$ — высота треугольника $ABC$. По условию угол $BAC$ равен 45°, поэтому $BH$ = $AH$. В треугольнике $CBH$ катет $BH$ лежит против угла 30°, поэтому $BC$ = 2$BH$. Медиана $HM$ прямоугольного треугольника $BHC$ равна половине гипотенузы $BC$.
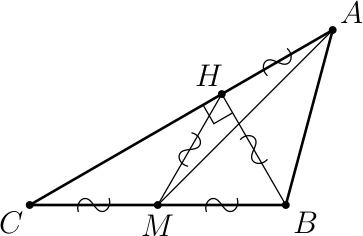
Собирая все равенства отрезков воедино, получаем $AH$ = $BH$ = $HM$ = $MB$ = $MC$. Значит, треугольник $MBH$ равносторонний, и угол $CMH$ равен 120°. Кроме того, треугольник $AHM$ равнобедренный, его угол $AHM$ равен 90° + 60° = 150°, поэтому угол $AMH$ равен 15°. Таким образом,
$∠AMC$ = $∠AMH$ + $∠HMC$ = 120° + 15° = 135°.

