Всероссийская олимпиада школьников по математике, 9 класс, 2017 год
дата проведения: 16 октября 2017 - 22 октября 2017
Задача 4.
Два квадрата имеют общую вершину. Найдите отношение отрезков $AB$ и $CD$, показанных на рисунке.
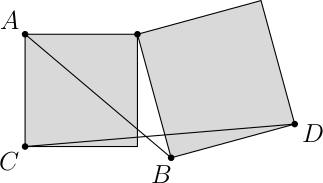
Ответ на Задачу 4.
Ответ: 1 : $\sqrt{2}$.
Решение:
Пусть точка $O$ — общая вершина двух квадратов, а их стороны равны $a$ и $b$. Диагонали квадратов равны $\sqrt{2}a$ и $\sqrt{2}b$ соответственно. Кроме того, $∠COD$ = $∠COB$ + $∠BOD$ = $∠COB$ + 45° = $∠COB$ + $∠AOC$ = $∠AOB$. Треугольники $AOB$ и $COD$ подобны по общему углы и пропорциональным сторонам при этом угле.
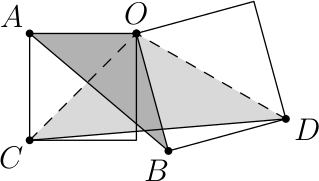
Следовательно, $AB$ : $CD$ = 1 : $\sqrt{2}$.

