Задача 1.
45 конфет стоят столько же рублей, сколько их можно купить на 20 рублей. Сколько конфет можно купить на 50 рублей?
Задача 2.
Женя расставил по кругу числа от 1 до 10 в некотором порядке, а Дима в каждой промежуток между числами вписал их сумму. Могло ли так случиться, что все написанные Димой числа оказались различными?
Задача 3.
Можно ли в некоторые клетки таблицы 8 × 8 написать единицы, а в остальные — нули, так, чтобы во всех столбцах была разная сумма, а во всех строчках — одинаковая?
Задача 4.
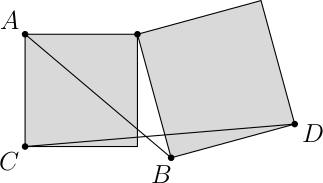
Два квадрата имеют общую вершину. Найдите отношение отрезков $AB$ и $CD$, показанных на рисунке.
Задача 5.
Числа $a$, $b$, $c$ и $d$ таковы, что $a$ + $b$ = $c$ + $d$ ≠ 0, $ac$ = $bd$. Докажите, что $a$ + $c$ = $b$ + $d$.
Задача 6.
Вдоль трассы стоят 60 дорожных знаков. На каждом из них написана сумма расстояний до оставшихся 59 знаков. Возможно ли такое, что на знаках написаны 60 различных натуральных чисел? (Расстояния между знаками не обязательно целые)

