Задача 4.
Квадрат $ABCD$ вписан в окружность ω. На меньшей дуге $CD$ окружности ω выбрана произвольная точка $M$. Внутри квадрата отмечены такие точки $K$ и $L$, что $KLMD$ — квадрат. Найдите $∠AKD$.
Ответ на Задачу 4.
Ответ: 135°.
Решение:
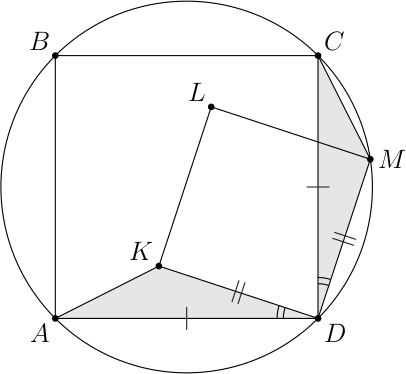
Докажем равенство треугольников $DAK$ и $DCM$. Проверим, что выполнены условия первого признака равенства треугольников. Отрезки $DA$ и $DC$ равны как стороны квадрата $ABCD$, отрезки $DK$ и $DM$ равны как стороны квадрата $KLMD$. Далее, поскольку углы $ADC$ и $KDM$ исходных квадратов прямые, можно записать:
$∠ADK$ = 90° − $∠KDC$ = $∠CDM$
Таким образом, треугольники $DAK$ и $DCM$ действительно равны. Следовательно, $∠AKD$ = $∠CMD$. Но $∠CMD$ = 135°, так как он вписанный и опирается на дугу $DABC$ окружности ω, а мера этой дуги равна 270°. Тогда $∠AKD$ = 135°, что и требовалось найти.

