Всероссийская олимпиада школьников по математике, 8 класс, 2018 год, 2 этап
дата проведения: 11 октября 2018 - 21 октября 2018
Задача 6.
Выпуклый четырёхугольник $ABCD$ таков, что $∠BAC$ = $∠BDA$ и $∠BAD$ = $∠ADC$ = 60°. Найдите длину $AD$, если известно, что $AB$ = 14, $CD$ = 6.
Ответ на Задачу 6.
Ответ: 20.
Решение:
Продлим $AB$ и $CD$ до пересечения в точке $P$. Поскольку $∠P AD$ = $∠ADP$ = 60°, то треугольник $ADP$ является равносторонним. Далее заметим, что треугольник $AP C$ равен треугольнику $DAB$, поскольку $AP$ = $AB$, $∠APC$ = 60° = $∠DAB$ и $∠PAC$ = $∠ADB$ (см. рисунок).
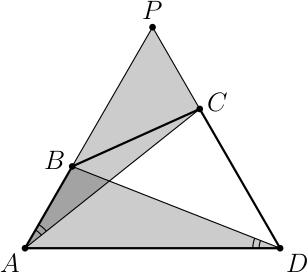
Поэтому $PC$ = $AB$ = 14, и $AD$ = $PD$ = $PC$ + $CD$ = 14 + 6 = 20.

