В числовом выражении некоторые цифры заменили буквами (разные цифры — разными буквами, одинаковые цифры — одинаковыми буквами). Получилось следующее:

2018A : BCD = AA

Какое числовое выражение было записано изначально? (Достаточно привести пример. 2018A изначально было пятизначным числом.)

В мешке у Деда Мороза находятся меньше ста подарков для Пети, Вася, Бори и Лёши. Дед Мороз отдал половину подарков Пете, пятую часть — Васе, седьмую часть — Боре. Сколько подарков досталось Лёше?

Карина достала из коробка несколько спичек и собрала из них сетку 3 × 7 из квадратиков со стороной в одну спичку, как на рисунке ниже.

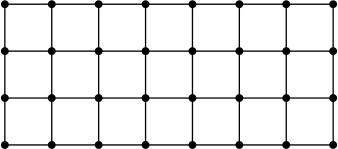
Какое минимальное количество спичек ей нужно ещё достать из коробка, чтобы из всех спичек она смогла собрать сетку в форме квадрата? (Квадратики сетки опять должны иметь сторону в одну спичку. Лишних спичек остаться не должно.)

На школьном спектакле все 25 мест в первом ряду заняты школьниками. Известно, что

• никакие две девочки в этом ряду не сидят рядом;
• рядом с каждым мальчиком сидит ещё хотя бы один мальчик;
• всего в первом ряду сидят 9 девочек.

Могло ли так оказаться, что на центральном месте в ряду сидит мальчик? (Ответ обоснуйте.)

По определению n! = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n. Докажите, что выражение 1008! ⋅ 1009! ⋅ 2017! ⋅ 2018! не является квадратом натурального числа.

Выпуклый четырёхугольник $ABCD$ таков, что $∠BAC$ = $∠BDA$ и $∠BAD$ = $∠ADC$ = 60°. Найдите длину $AD$, если известно, что $AB$ = 14, $CD$ = 6.